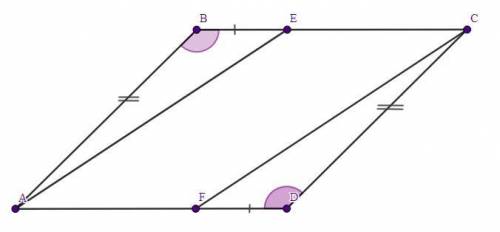
Четырёхугольник ABCD - параллелограмм.
ВЕ = DF (Е ⊂ ВС, F ⊂ AD).
Доказать :Четырёхугольник AECF - параллелограмм.
Доказательство :В параллелограмме противоположные углы и противоположные стороны равны между собой (свойство параллелограмма).Отсюда следует, что ∠В = ∠D, АВ = CD.
Рассмотрим ΔАВЕ и ΔCDF.
ВЕ = DF (по условию)
∠В = ∠D, АВ = CD (по выше сказанному) ⇒ ΔАВЕ = ΔCDF по двум сторонам и углу между ними (первый признак равенства треугольников).
Из равенства треугольников следует и равенство сторон АЕ и CF.
AD = BC (по свойству параллелограмма), но в своё очередь AD = BE + EC ; BC = DF + AF. Учитывая равенство из условия получаем, что ЕС = AF.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм (свойство параллелограмма).АЕ = CF ; ЕС = AF (по выше сказанному) ⇒ четырёхугольник AECF - параллелограмм.
ответ :Что требовалось доказать.
1)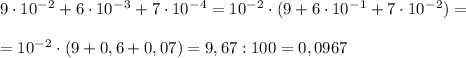
2)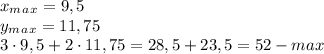
3)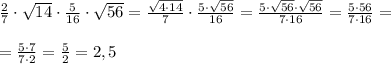
Ну и, как "Лучшее решение" не забудь отметить, ОК?!... ;)))