ответ: два решения (одно для остроугольного треугольника, другое для тупоугольного...)
1) Р = 256 (см)
2) Р = 56V21 (см)
Объяснение: треугольник АВС, основание ВС=2а (чтобы не возиться с дробями); АВ=АС=b
P = 2a+2b = 2(a+b)
а=b*cos(B); по т.синусов: b=2R*sin(B)
S = 2a*h/2 = ah; h = b*sin(B)
S = P*r/2 = (a+b)*r
(a+b)*r = ab*sin(B)
b(1+cos(B))*r = b*b*sin(B)*cos(B)
(1+cos(B))*r = 2R*sin^2(B)*cos(B)
r/(2R) = (1-cos(B))*cos(B)
обозначим х=cos(B)
x^2 - x + (6/25) = 0
(5x)^2 - 5*(5x) + 6 = 0
по т.Виета корни (3) и (2)
5х=3 ---> х = 0.6
---> sin(B) = V(1-0.36) = 0.8 или
5х=2 ---> х = 0.4
---> sin(B) = V(1-0.16) = 0.2V21
b = 2*50*0.8 = 80 или
b = 2*50*0.2V21 = 20V21
a = 80*0.6 = 48 или
а = 20V21*0.4 = 8V21
P = 2*(80+48) = 128*2 = 256 или
Р = 2*(20+8)*V21 = 56V21
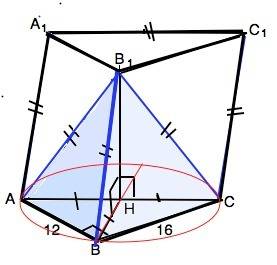
Грань АА1С1С - квадрат.
АС по т.Пифагора равна 20. В призме все боковые ребра равны. ⇒ ВВ1=СС1=АА1=АС=20.
По условию боковые ребра пирамиды АВ1СВ равны, значит, их проекции равны между собой и равны радиусу окружности, описанной около основания АВС. ⇒
Вершина пирамиды В1 проецируется в центр Н описанной около прямоугольного треугольника окружности, т.е. лежит в середине гипотенузы.
∆ АВС прямоугольный, R=АС/2=10.
АН=СН=ВН=10.
Высота призмы совпадает с высотой В1Н пирамиды.
По т.Пифагора
В1Н=√(BB1²-BH²)=√(20²-10²)=√300=10√3
Формула объёма призмы
V=S•h где S - площадь основания, h - высота призмы.
S-12•16:2=96 (ед. площади)
V=96•10√3=960√3 ед. объёма.
№1. Треугольники ВКМ и BKN равны по стороне и двум прилежащим углам.
Значит BM = BN. Значит тр-ки BMN и АВС подобны по 1 признаку подобия(по 2-м пропорциональным сторонам и углу между ними.)
Значит у них равны все углы, то есть MN||АС, значит MN перпендикулярно ВК,
что и требовалось доказать.
Угол BNK = углу BMK = 110 град. (из равенства тех же тр-ов: BKM и BKN).
№2. Во влажениях!
№3. В Δ АВС угол АВС равен
90-15=75°
ВΔ ВАД угол АВД равен
75-15=60
ВДА=90-60=30°
АВ, как противолежащая углу 30, равна половине ВД.
ВД=2*3=6 см
Рассмотрим Δ ВДС.
В нем равные углы при основании ВС.
Поэтому Δ ВДС - равнобедренный.
ДС=ВД=6 см.
Сумма двух сторон треугольника должна быть больше третьей стороны.
Сторона ВД+ДС=12см
ВС < 12см
Длина стороны ВС не может быть равна 12 см