Доказательство:
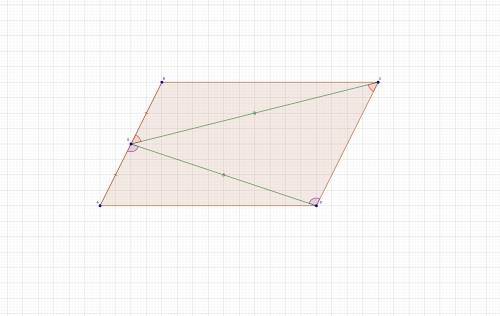
Т.к. ABCD - параллелограмм, то AB//CD и AD//BC.
∠ECD = ∠CEB как накрест лежащие при параллельных прямых AB и CD и секущей EC.
∠EDC = ∠DEA как накрест лежащие при параллельных прямых AB и CD и секущей ED.
Т.к. EC = ED , то ΔECD - равнобедренный с основанием CD.
Значит ∠ECD = ∠EDC как углы при основании.
Следовательно ∠CEB = ∠DEA
ΔEBC = ΔEAD по двум сторонам и углу между ними (EB = EA по условию.)
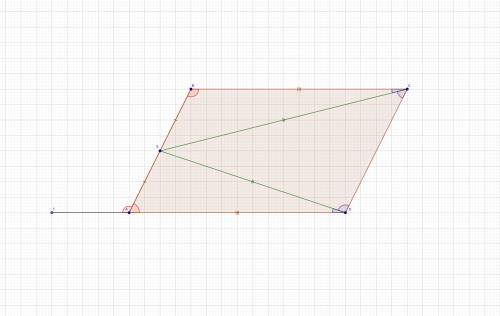
См. рисунок 2.
Из равенства треугольников EBC и EAD следует, что ∠EBC = ∠EAD
и ∠BCE = ∠ADE
∠BCD = ∠BCE + ∠ECD
∠ADC = ∠ADE + ∠EDC
Следовательно ∠BCD = ∠ADC
Продолжим сторону AD влево.
∠FAB = ∠ABC как накрест лежащие при параллельных прямых AD и BC и секущей AB.
∠FAB = ∠ADC как соответственные при параллельных прямых AB и DC и секущей AD
Собирая все вместе получаем, что ∠ABC = ∠BCD = ∠CDA = ∠DAB
Получается, что ABCD - параллелограмм в котором все углы равны. Следовательно ABCD - прямоугольник
Пронумеруем острова.
Заметим, что на остров В нужно приходить со стороны 20 острова, так как в противном случае мы попадем на остров В, не побывав на 20 острове.
По тем же причинам на 15 остров нужно приходить со стороны 10 острова.
Далее, на 4 остров нужно приходить со стороны 3 острова.
На 7 остров нужно приходить со стороны 8 острова, иначе траектория замкнется до того момента как все острова попадут в маршрут.
На 8 остров нужно приходить со стороны 9 острова, иначе он не попадет в маршрут. С 11 острова нужно следовать в сторону 16 острова.
С 22 острова нужно следовать в сторону 23 острова, чтобы включить его в маршрут.
Далее маршрут достраивается единственным образом. С острова С необходимо двигаться на восток.
ответ: Г) на восток