ответ: 40,4 (ед. длины)
Объяснение:
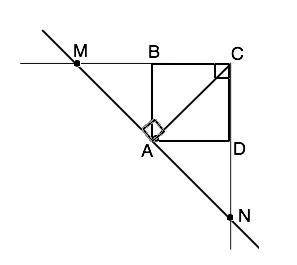
Диагонали квадрата являются его биссектрисами и делят его углы на два по 45°. СА перпендикулярна MN (дано), ⇒треугольники МАС и САN - прямоугольные. Поэтому градусная величина углов СМA и CNA – 45°, они равны между собой. Отсюда треугольники СМA и CNA прямоугольные равнобедренные (углы при их основаниях СМ и СN равны) с общим катетом СА. Они равны между собой. МС=СN, МА=NА. Треугольник МСN равнобедренный, отрезок СА для треугольника СМN является медианой и равен половине гипотенузы MN. ⇒ MN=2•CA=2•20,2=40.4 ед. измерения.
Найдите площадь треугольника, две стороны которого равны 6 и 8, а медиана, заключённая между ними, равна 5.
▔ ▔ ▔
★☆★ Чертёж смотрите во вложении ★☆★
Дано:ΔАВС.
АВ = 6.
ВС = 8.
ВО — медиана = 5.
Найти:S(ΔАВС) = ?
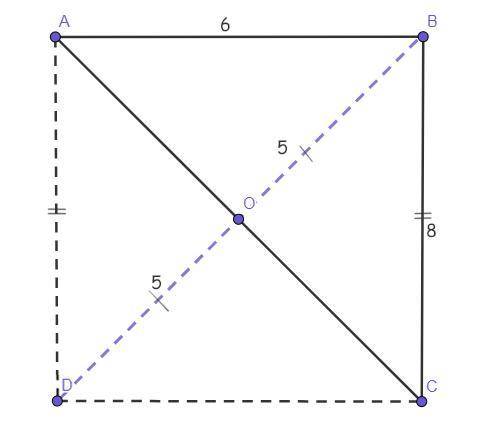
Решение:Достроим ΔАВС до параллелограмма ABCD как показано на рисунке.
▸Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам◂
Следовательно —
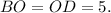
Тогда —
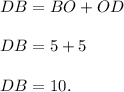
▸Противоположные стороны параллелограмма равны◂
AD и ВС — противоположные стороны.
Следовательно —
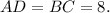
Рассмотрим ΔABD.
▸Если сумма квадратов двух сторон равна квадрату большей стороны, то такой треугольник — прямоугольный (теорема, обратная теореме Пифагора)◂
Проверим стороны ΔABD —
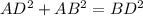
Подставим известные нам численные значения —
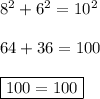
Мы получили верное равенство, следовательно, ΔABD — прямоугольный (∡A = 90°).
▸Если в параллелограмме один угол прямой, то этот параллелограмм — прямоугольник◂
То есть, параллелограмм ABCD — прямоугольник.
Тогда, по определению прямоугольника —
∡А = ∡В = ∡С = ∡D = 90°.
Рассмотрим ΔАВС — прямоугольный.
▸Площадь прямоугольного треугольника равна половине произведения его катетов◂
Следовательно —
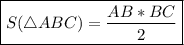
Подставим в формулу известные нам численные значения —
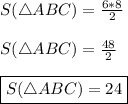
24 (ед²).
Параллелограмм АВСД, ВН высота на АД, ВК - высота на СД,
треугольник АВН прямоугольный, угол АВН=х, угол ВАН = 90-х
треугольник КВС прямоугольный, угол С=углуА=90-х, угол КВС= 90 - уголС=90-(90-х)=
=х, угол АВС = 180-уголВАН = 180-(90-х) =90+х, угол НВД = угол АВС - уголАВН-уголКВС =
=90+х-х-х=90-х
уголВАН=углуНВД=90-х