Получили прямоугольный треугольник, одним катетом АС которого является перпендикуляр, а наклонная АВ является гипотенузой, проекция на плоскость ВС - это второй катет. Ищем его по теореме Пифогора.
√(81-36)=√45см
Получили треугольник АВС, в котором АС=6см, АВ=9см, ВС=√45см
Из вершины прямого угла С проводим перпендикуляр СН на гипотенузу АВ. АН - это и есть проекция перпендикуляра АС на наклонную АВ. Можно решать через подобие полученных треугольников, но лучше по теореме Пифагора.
Пусть ВН=х, тогда АН=9-х
Из треуг. АНС: CH^2=36-(9-x)^2
Из треуг. СНВ: CH^2=45-x^2
Приравниваем:
36-(9-x)^2=45-x^2
36-81+18х-x^2==45-x^2
18x=90
x=5
CH=√(45-25)=√20=2√5см
Відповідь:
Пояснення:
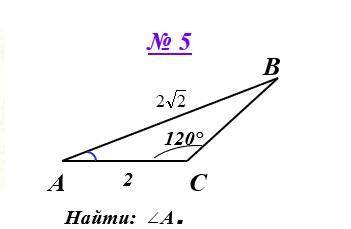
a/sinA=c/sinC=b/sinB
Угол В=180-120-А=60-А
2sgr(2)/sin(180-60) = 2/sin(60-A)
sin(60-A)=1/2×sqr(3)/sqr(2)=0,61
A=60-arcsin 0,61