Можно объяснить, почему высота прямоугольного треугольника равна произведению проекций катетов на гипотенузу?
Можно. Только не высота равна, а ее квадрат. И Вы сами наверняка не раз выводили это свойство при решении задач.
Высота прямоугольного треугольника, проведенная из вершины прямого угла,
есть среднее пропорциональное между отрезками, на которые делится
гипотенуза этой высотой.
Оно выведено из подобия треугольников, на которые высота, проведенная к гипотенузе,
делит исходный прямоугольный треугольник. Рассмотрим треугольники АСН и СНВ
Смотрим рисунок.
∠ АСН=90 -∠НСВ
∠ НВС=90 -∠НСВ
Если в прямоугольных треугольниках есть равные острые углы, то такие треугольники подобны.
Треугольники АНС и СНВ подобны
Меньший катет АН первого треугольника относится к меньшему катету СН второго треугольника,
как больший катет СН первого относится к большему катету НВ - второго.
АН:СН=СН:НВ
АН·НВ=СН²,
.
а АН и НВ - это и есть проекция катетов на гипотенузу
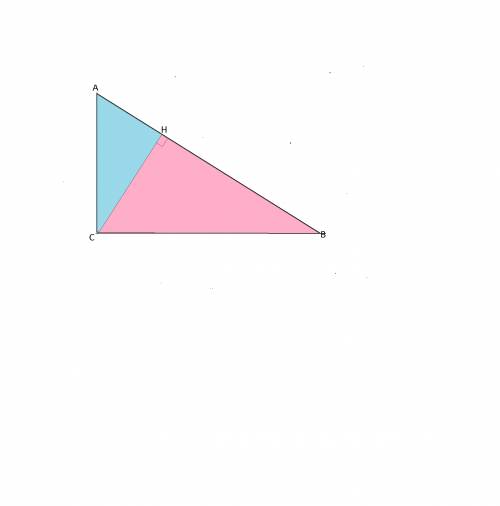
Стороны Δ АВС равны АС=12 м, ВС=16 м и АВ=20 м, СН - высота.
Для данных величин выполняется равенство:
20² = 12² + 16²
400 = 144 + 256
400 = 400
тогда по теореме, обратной теореме Пифагора, данный треугольник - прямоугольный. Большая сторона АВ - гопотенуза = 20, .
Тогда высота СН , проведенная из вершины прямого угла С, опущена на гипотенузу АВ и делит треугольник на два подобных треугольника, каждый из которых подобен Δ АВС.
Рассмотрим подобие треугольников АСН и АВС:
СН/СВ = АС/АВ
СН/16 = 12/20
СН = 16*12/20
СН = 48/5
СН = 9,6
ответ: высота равна 9,6 м.
У моей сестры такая же задача)