Задача 1 (рисунок 1).
1) МВ и КВ, МА и ТА, КС и ТС - отрезки касательных, проведённых из одной точки. Они равны по свойству касательных. Следовательно, треугольник АВС разбивается на три пары равных (попарно) отрезков.
PΔАВС=2*2+4*2+6*2=24см.
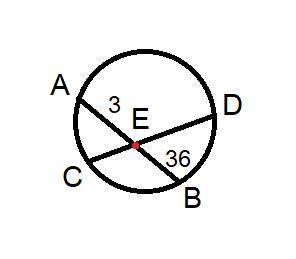
Задача 2 (рисунок 2).
3:4=3х+4х
По теореме о пересекающихся хордах:
36*3=3х*4х
108=12х²
х=3.
CD=3*7=21см.
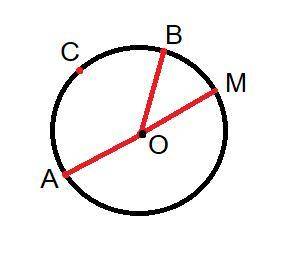
Задача 3 (рисунок 3).
Сначала ищем градусную меру дуг АМВ и АСВ.
Если 2 дуги, на которые делит окружность любая хорда, вместе равны 360°, то:
(360-80):2=140° - дуга АСВ.
Тогда дуга АМВ = 140+80=220°. (в сумме 360).
Дальше пользуемся свойствами вписанных и центральных углов:
1) ∠АСВ=150°, ∠АОВ=210° (центральные ∠).
2) ∠АМВ=половине АОВ=75°, ∠АВМ=половине АОМ=90°,
3)∠АСВ=половине АМВ=105° (вписанные углы).
ответ: 210° - ∠АМВ, 90° - ∠АВМ, 105° - ∠АСВ.
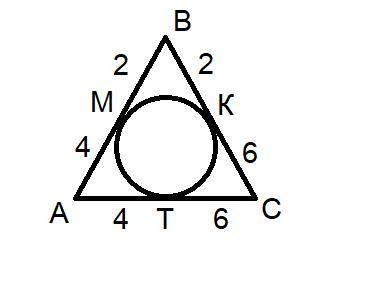
Объяснение:
Соединим радиусы с касательными и получим прямоугольные треугольники.
КО=ОМ=3
Рассмотрим ∆АОМ;
АО- гипотенуза
ОМ- катет против угла 30°
АО=2*ОМ=2*3=6
Теорема Пифагора
АМ=√(АО²-ОМ²)=√(6²-3²)=√(36-9)=√27=
=3√3
АМ=АК, свойство касательных проведенных из одной точки.
АК=3√3;
АО- биссектрисса угла <КАМ
<КАМ=2*<ОАМ=2*30°=60°
Рассмотрим ∆АВС.
Сумма острых углов прямоугольного треугольника равна 90°
<В=90°-<САВ=90°-60°=30°
AC=CK+KA=3+3√3
tg<B=AC/CB
tg30°=1/√3
1/√3=(3+3√3)/CB
CB=√3(3+3√3)=3√3+3*3=3√3+9
S(∆ABC)=1/2*AC*CB=1/2*(3√3+9)(3+3√3)=
=1/2(9√3+27+27+27√3)=1/2(54+36√3)=
=1/2*2(18√3+27)=18√3+27
ответ: 18√3+27
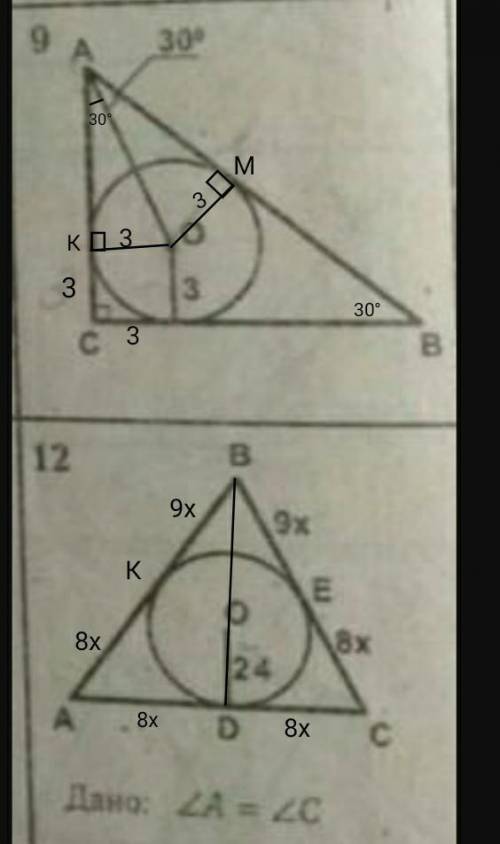
Задача 2)
Треугольник ∆АВС- равнобедренный
АВ=ВС, так как углы при основании равны, <А=<С по условию.
ЕС=СD, свойство касательных
ВЕ=ВК, свойство касательных
Так как треугольник равнобедренный, то
АК=АD=DC=CE.
AC=8x*2=16x
AB=BC=9x+8x=17x
Формула нахождения радиуса
r=AC/2√((2*AB-AC)/(2AB+AC))=
=16x/2√((2*17x-16x)/(2*17x+16x))=
=8x√((34x-16x)/(34x+16x))=8x√(18x/50x)=
=8x√(9/25)=8x*3/5=24x/5=4,8x
r=4,8x
r=24
4,8x=24
x=24/4,8
x=5
AB=17x=17*5=85
AC=16x=16*5=80
AD=AC/2=80/2=40
Теорема Пифагора
ВD=√(AB²-AD²)=√(85²-40²)=√(7225-1600)=
=√5625=75
S(∆ABC)=1/2*BD*AC=1/2*75*80=3000
ответ: 3000 ед²
Все по той же схеме, как и если соединены середины сторон.
Пусть К лежит на АВ, L на ВС, M на CD, N на AD.
Тогда - к примеру - треугольники ABD и AKN подобны (стороны их общего угла BAD пропорциональны) поэтому равны углы AKN и ABD, то есть KN II BD.
Точно так же доказывается, что LM II BD, LK II AC, MN II AC.
То есть противоположные стороны четырехугольника KLMN параллельны. ЧТД