площадь трапеции равна 63cos31° +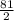 
sin62° , что приблизительно равно 89.76
Объяснение:
Достроим рисунок высотами BE и CF.
Отметим, что площадь трапеции ABCD будет совпадать с площадью прямоугольника AFCG = AF*CF = (AE+EF)*BE = (7+AE)*BE
∠ABC=∠CBD=121° , ∠EBC=90° значит ∠ABE=31°
В прямоугольном треугольнике ABE
sin∠ABE=AE/AB ⇒ sin31°=AE/9 ⇒ AE=9*sin31°
cos∠ABE=BE/AB ⇒ cos31°=BE/9 ⇒ BE=9*cos31°
Значит искомая площадь = (7+AE)*BE = (7+9*sin31°)*9*cos31° =
= 63cos31° + 81sin31°cos31° = 63cos31° + 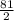sin62° ≈ 89.76
Объяснение:
Ромб - это параллелограмм, у которого все стороны равны. Диагонали ромба взаимно перпендикулярны; и точкой пересечения делятся пополам. Найдём сторону ромба по т. Пифагора:
а=√(8²+16²)=√(64+256)=√289=17 см.
Периметр ромба находится по формуле Р=4а, где а - сторона ромба. Зная сторону ромба, найдём его периметр:
Р=4а=4*17=68 см.