АСВ и DBE подобны, площади их 4+5=9 и 4, значит стороны относятся, как √(9/4) = 3/2. DE = 7, значит АС = 7*3/2 = 10,5
ответ:Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Объяснение:Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
Через дві твірні конуса, кут між якими β, проведено площину. Площа
бічної поверхні конуса дорівнює S. Знайдіть площу перерізу, якщо твірна
конуса утворює з висотою кут α.
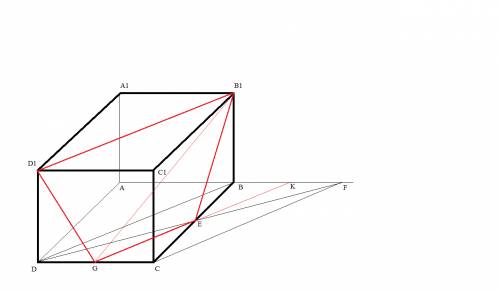
сделаем построение по условию
точка G - середина отрезка CD
точки B1, D1,G образуют плоскость GB1D1
дополнительные построения
прямая (BD) параллельна (B1D1)
прямая (CF) параллельна (BD)
прямая (GK) параллельна (BD)
прямая (CB) -секущая для параллельных прямых (BD) ,(GK), (CF)
по теореме Фалеса, прямая (CB) отсекает пропорциональные отрезки DG=GC и CE=EB
по теореме Пифагора
GE^2 = GC^2+CE^2=(D1C1/2)^2+(B1C1/2)^2 =( (D1C1)^2+(B1C1)^2 )/4 = (B1D1)^2 / 4
GE = B1D1/2 - отрезки GE и B1D1 НЕ РАВНЫ
прямая (GK) параллельна (BD) , а значит и (B1D1) и проходит через точку G в плоскости GB1D1
следовательно прямая (GK) принадлежит плоскости GB1D1
точка E - пересечение (GK) и (CB)
точки Е и B1, а значит и отрезок EB1 принадлежат плоскости GB1D1
искомое сечение - четырехугольник GD1B1E ,
противоположные стороны B1D1 и EG параллельны и не равны.
Основной признак ТРАПЕЦИИ:
четырёхугольник является трапецией, если его параллельные стороны не равны.
ДОКАЗАНО
Отношение площадей треугольников равно квадрату коэффициента подобия
SABC=SDBE+SADEC=(4+5)=9 см^2.
Отношение AC/DE=AC/7=k => SABC/ SDBE=9/4=k^2 => k=3/2.
Тогда AC/7=3/2 => AC=21/2=10,5 см