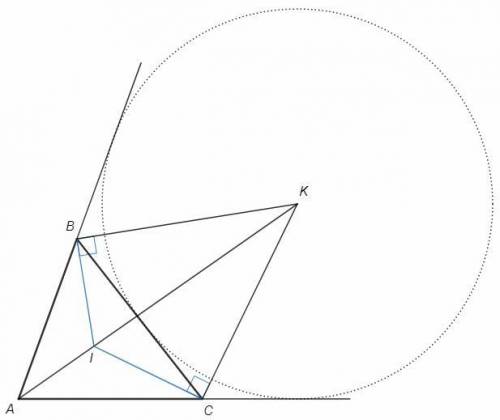
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в одной точке. (Вневписанная окружность также вписана во внутренний угол, следовательно ее центр лежит биссектрисах всех трех углов.)
CK - биссектриса внешнего угла. Требуется найти угол между биссектрисами внешних углов (BKC).
Для этого найдем угол между биссектрисами внутренних углов. Пусть I - точка пересечения биссектрис внутренних углов ABC.
A +B +C =180
BIC +B/2 +C/2 =180
BIC= 90 +A/2
Угол между биссектрисами внешнего и внутреннего углов - прямой. (Внешний и внутренний углы - смежные. Сумма смежных углов 180, следовательно сумма их половин 90.)
Сумма противоположных углов четырехугольника BICK равна 180, следовательно сумма двух других углов также 180.
BIC +BKC =180
BKC= 90 -A/2
A=70, BKC=90-35=55
Одна из формул площади параллелограмма Ѕ=a•h. Очевидно, что при одинаковой площади большей будет высота, проведенная к меньшей стороне, и наоборот. Следовательно, искомой будет высота к стороне АВ ( или равной ей CD).
На рисунке в приложении высота к меньшей стороне АВ пересекается с ее продолжением. Из прямоугольного треугольника AKD высота DK=AD•sinA=6•1/3=2 (ед. длины)
Как вариант можно найти большую высоту иначе. Сначала найти длину меньшей высоты ВН=АВ•sinA, затем найти площадь S=ВН•AD и высоту DK=S:AB.