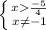
Объяснение:
^ - возведение в степень
1. Площадь параллелограмма равна произведению стороны и проведённой к ней высоты. Значит, S = BC * BH.
S = 20см * 5см = 100см^2
2. Площадь прямоугольного треугольника равна половине произведения катетов. Так как в условии сказано, что угол B = 90, то можно сказать, что проведённые из этого угла стороны BK и BD - катеты по определению. Значит, S = (BK * BD) / 2.
S = (50см * 2см) / 2 = 50см^2
3. По теореме Пифагора: AC^2 + AB^2 = CB^2.
AC^2 = BC^2 - AB^2.
AC^2 = 32.
AC = 4V2 (V - квадратный корень)
4. По формуле Герона: S = Vp(p-a)(p-b)(p-c), где p - полупериметр. Он равен 16 см. Вычисляем площадь. S = V2304
S = 48
Теперь, зная, что площадь треугольника равна половине произведения высоты на сторону, вычисляем высоту/ S = (a * b) / 2
Получаем три высоты: 9,6см; 9,6см; 8см.
5. Площадь ромба равна половине произведения диагоналей (мало где говорится, но это можно вывести из формул площадей других фигур) S = (5см * 12см) / 2 = 30см^2.
Диагонали ромба делят его на 4 равных прямоугольных треугольника, катеты которых равны половинам диагоналей. Т.е. если взять один из таких треугольников, два его катета будут равны 2,5см и 6см. Теперь вычисляем всё по той же теореме Пифагора гипотенузу или же сторону ромба. Она будет равна 6,5 см
№1
Объяснение:
Если четырёхугольник можно вписать в окружность, значит в этом четырёхугольнике сумма противолежащих углов равна 180° ⇒
⇒ угол, лежащий против угла в 120° равен 180° - 120° = 60° и угол, лежащий против угла в 150°, равен 180° - 150° = 30°
Так как вершины четырёхугольника лежат на окружности, его углы будут являться вписанными и отсюда, градусные меры дуг, на которые эти углы опираются, будут в два раза больше самих углов.
Находим, что углы в 60° и 30° четырёхугольника опираются на дуги в 120° и 60°
№2 (фото)
№3 ответ:4
№4ОЕ⊥СD⇒ ОЕ - радиус.
АВ⊥ВС и АD
Проведем OK⊥АВ
ОК=r
OH⊥AD
АН=ОК=OE=6
HD=ED=9
AD=AH+HD=15
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
Трапеция - четырехугольник.
ВС+AD=AB+CD
Р=ВС+AD+AB+CD=2•(10+15)=50 см
——————————————————
4. На рис. 134 точка О – центр вписанной окружности, угол А=углу С, BD=18 см, BO:OD=5:4. Найдите стороны треугольника.
DO+ВО=9х ⇒
х=18:9=2
OD=8, ВО=10.
По условию углы при АС равны. ⇒ ∆ АВС - равнобедренный, АВ=ВС.
Центр вписанной в треугольник окружности лежит на биссектрисе.
Биссектриса равнобедренного треугольника - высота и медиана. ⇒
∠BDA=90°
AD=CD.
Проведем ОН - перпендикуляр в точку касания на АВ.
Из ∆ ВОН по т.Пифагора ВН=6
В прямоугольных ∆ АВD и ∆ OBH острый угол при В общий.⇒
∆ АВD~∆ OBH
Из подобия следует отношение
АВ:ВО=ВD:BH
AB•6=10•18⇒
AB=180:6=30
По т.Пифагора AD=24 ⇒
АС=48
ВС=АD=30
№5В чотирикутник можна вписати коло тоді й тільки тоді, коли суми його протилежних сторін рівні.
Таким чином,
AB+CD= BC+AD;
10+7= 8+AD;
17=8+AD;
AD= 17-8;
AD= 9.
Відповідь: якщо AD=9 см, то в даний чотирикутник можна вписати коло.
№6если трапеция описана около окружности, то сумма оснований равна сумме боковых сторон, а средняя линия равна полусумме оснований,тогда средняя линия = (5+7)/2=6
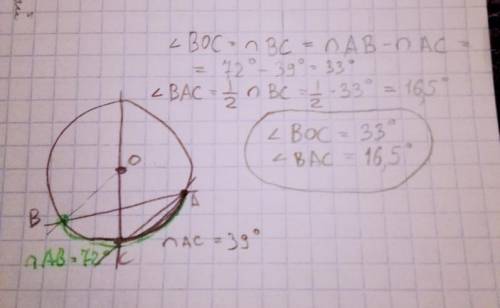
Промахнулись немного, это не геометрия...
4x+5 > 0
4x > -5
x > -5/4