l=2ПR
Для начала можно попробовать доказать ,что треугольник прямоугольны е
8^2+15^2=17^2
64+225=289
Следовательно треугольник прямоугольный
Т.к. треугольник прямоугольный то радиус описанной окружности равен половине гипотенузы,то есть в нашем случае 8,5
l=2*8.5П=17П
Объяснение:
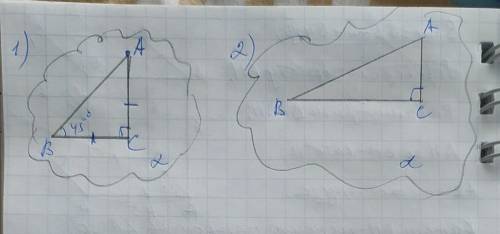
1) позначемо похилу АВ, проекцію ВС, відстань від точки А до площини - АС - отримаємо прямокутний трикутник АВС, в якому ВС і АС - катети, а АВ - гіпотенуза. Якщо ВС=АС, тоді отриманий трикутник АВС - рівнобедренний, тому його кути при основі АВ - рівні. Так як сума гострих кутів прямокутного трикутника дорівнює 90°, тоді кутА=кутВ=90÷2=45°
ВІДПОВІДЬ: кутВ між площиною та похилою дорівнює 45°
2) Так само позначемо кути, як у першому завданні АВС, і якщо катет АС дорівнює половині гіпотенузи АВ, тоді АС лежить навпроти кута В=30°(властивість кута 30°),
ВІДПОВІДЬ: кутВ=30°
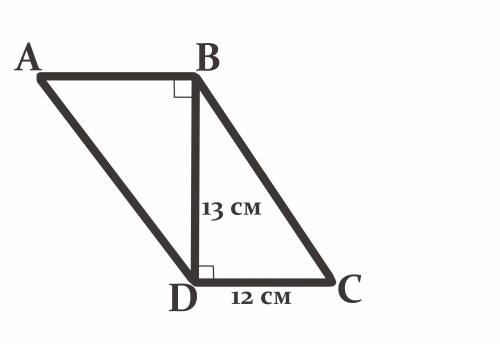
Дано :
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
Покажем, что данный треугольник является прямоугольным
17*17=289
15*15=225
289-225=64=8*8
Выполняется теорема Пифагора.
L=17П