3.Дано ABC -рівнобедрений AB = BC . Зовнішній кут при вершині А дорівнює 150° . Знайдіть внутрішні кути трикутника.

3.Дано ABC -рівнобедрений AB = BC . Зовнішній кут при вершині А дорівнює 150° . Знайдіть внутрішні к

👇

Увидеть ответ

Ответ:

demidvashenko

29.01.2021

АВ=ВС, но на рисунке АС=СВ

сделаем как на рисунке обозначено

внешний угол равен сумме двух внутренних, не смежных с ним углов(С+В)

С+В=150°

угол САВ - смежный с углом САМ и равен

180°-150°=30°

Так как треугольник равнобедренный, то углы при основании АВ равны

угол А=30°

угол В=30°

Находим угол С

С+30°=150°

С=120°

4,4(19 оценок)

Открыть все ответы

Ответ:

Аляска56

29.01.2021

68. По данным на рисунке найдите площадь 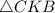$\triangle CKB$ .

- - -Дано :

ΔСКВ - прямоугольный (∠С = 90°).

СК - высота (СК⊥АВ).

АК = 4, КВ = 16.

Найти :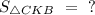 $S_{\triangle CKB} ~=~ ?$ Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

Следовательно, 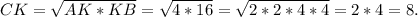$CK = \sqrt{AK*KB} = \sqrt{4*16} = \sqrt{2*2*4*4} = 2*4 = 8.$

Площадь прямоугольного треугольника равна половине произведения его катетов.

Следовательно, 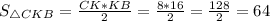$S_{\triangle CKB}=\frac{CK*KB}{2} =\frac{8*16}{2} =\frac{128}{2} =64$ ед².

ответ :

64 ед².

- - -

70. ABCD - прямоугольник. Найдите 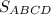$S_{ABCD}$ .

- - -Дано :

Четырёхугольник ABCD - прямоугольник.

АС - диагональ.

HD⊥АС.

HD = 6, АН = 9.

Найти :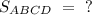

$S_{ABCD}~=~ ?$

Решение :Прямоугольник - это параллелограмм, все углы которого прямые.

Следовательно ∠D = 90°.

Рассмотрим ΔACD - прямоугольный.

В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

Следовательно, 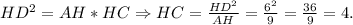$HD^{2} = AH*HC \Rightarrow HC = \frac{HD^{2} }{AH} = \frac{6^{2} }{9} = \frac{36}{9} =4.$

Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.

Следовательно, 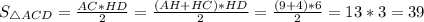$S_{\triangle ACD}=\frac{AC*HD}{2} =\frac{(AH+HC)*HD}{2} =\frac{(9+4)*6}{2} = 13*3=39$ ед².

Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.

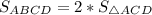Тогда $S_{ABCD} = 2*S_{\triangle ACD}$ = 2*39 ед² = 78 ед².

ответ :

78 ед².

4,5(52 оценок)

Ответ:

jessyss

29.01.2021

Географическое положение
Бразильское плоскогорье занимает большую часть востока Южной Америки от 3 до 35° ю. ш. , преимущественно в Бразилии, юг — в Уругвае, на юго-западе его край заходит в Парагвай и Аргентину. Сильно приподнято на востоке и юго-востоке над побережьем Атлантического океана. [5] Самая высокая точка здесь над уровнем моря - г. Пику-да-Бандейра (Pico da Bandeira), самая высокая вершина Бразильского плоскогорья и Бразилии. Высота 2890 м. Находится в массиве Капарао, между низовьями рек Параиба и Риу-Доси. Сложена гнейсами. Склоны покрыты влажнотропическими лесами. [4] На севере к Амазонской низменности и на юго-западе к Лаплатской низменности полого наклонено; на севера-запада обрывается к впадине верхнего Парагвая.
Геологическое строение
Бразильское плоскогорье состоит из древних кристаллических щитов и синеклиз, заполненных осадочными и вулканическими породами.

Древний Гвиано-Бразильский щит, составляющий основу Бразильского плоскогорья, сложен докембрийскими гнейсами и кристаллическими сланцами, пронизанными гранитоидами. Щит выступает на поверхность в виде Западно-Бразильского и Восточно-Бразильского выступов складчатого фундамента. Они разделены бассейнами Парнаиба (Мараньяо) и Сан-Франциско. Восточно-Бразильский выступ соответствует позднепротерозойской складчатой системе (байкалидам) , местами включающей более древние ядра. В начале кайнозоя меловая поверхность выравнивания здесь была приподнята, деформирована и нарушена разрывами, что привело к образованию блоковых гор. Сбросовые ступени образовали уступы. С обрывистой восточной стороны они иногда достигают высоты нескольких сот метров и производят впечатление настоящих хребтов ("серр"). От подножия такой серры местность к востоку постепенно повышается, а затем круто обрывается вниз, образуя новую серру.

4,6(26 оценок)

Это интересно:

Компьютеры-и-электроника

09.03.2021

Изучаем, как создать общедоступный календарь в Outlook...

Компьютеры-и-электроника

08.05.2020

Как получить очки отряда в Call of Duty Ghosts?...

Образование-и-коммуникации

29.04.2023

Как создать комиксы в стиле Манга...

Образование-и-коммуникации