Вравнобедренном треугольнике abc с основанием ac проведена биссектриса bd докажите чт точка m взятая на этой биссектрисе равноудаленна от вершин a и c можно с решением?

👇

Ответ:

dimaalexandrovi

27.05.2021

Биссектриса в этом треугольнике является медианой(уточни это в учебнике, я не припоминаю, какое именно это свойство).

А по определению медианы, AD=DC.

Т.к. в треугольниках ABD и CBD : BD - общая, а ABD=CBD- по условию, эти прямоугольные(это тоже нужно уточнить) треугольники равны. Следовательно, точка M на стороне BD будет равноудалена от вершин А и С, как соответсвующая точка в соответсвующих треугольниках)

4,4(93 оценок)

Открыть все ответы

Ответ:

Murew

27.05.2021

R≅5,04

H≅5,04

Объяснение:

Объём цилиндра :

(1) V = πR²H,

где R - радиус цилиндра, H - высота цилиндра.

Площадь полной поверхности цилиндра:

(2) S = πR² + 2πRH

Выразим из формулы (1) высоту цилиндра и подставим значение в формулу (2):

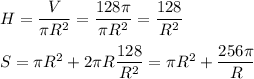
$H= \dfrac{V}{\pi R^{2} } =\dfrac{128\pi }{\pi R^{2} } =\dfrac{128}{R^{2} } \\\\S = \pi R^{2} +2\pi R\dfrac{128}{R^{2} } = \pi R^{2} + \dfrac{256\pi }{R}$

Найдём минимум этой функции по переменной R. Для этого вычислим производную и определим критические точки.

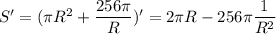$S' = (\pi R^{2} +\dfrac{256\pi }{R} )' = 2\pi R-256\pi \dfrac{1}{R^{2} }$ .

S' = 0,

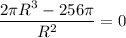
$\dfrac{2\pi R^3-256\pi }{R^{2} } = 0\\$

Если R = 0, то производная не существует.

$2\pi (R^3-128)=0\\\\R^3 = 128\\\\R=\sqrt[3]{128}$

R≅ 5.04

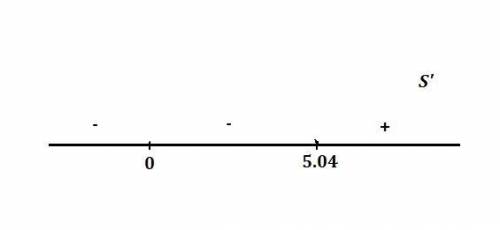
Отметим эти значения на координатной прямой и oпределим знак производной на трёх полученных числовых интервалах. (Cм.рис)

Известно, что в точке минимумa производная меняет знак с минусa на плюс. Соответственно, наименьшее количество материала можно получить, если радиус основания цилиндра R=5,04

Вычислим соответствующую высоту цилиндра:

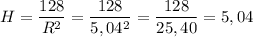
$H = \dfrac{128}{R^{2} } =\dfrac{128}{5,04^{2} } =\dfrac{128}{25,40} = 5,04$

Kаковы должны быть размеры открытого цилиндрического бака объёмом 128π, чтобы на его изготовление уш

4,6(77 оценок)

Ответ:

lisinpetr2014

27.05.2021

Всё просто. Рассмотрим треугольник ABD. Он является прямоугольным, т.к. AB перпендикулярна BD. Значит угол ABD равен 90 градусов. Известно, что один из углов равен 120 градусам, это самый большой угол паралеллограмма (очевидно, что это углы ABC и ADC). Из этого находим угол DBC. Он равен угол ABC-угол ABD=120-90=30. Углы DBC и BDA равны как накрест лежащие углы при параллельных прямых BC и AD. Аналогично равны углы ABD и BDC. AB - катет лежащий напротив угла 30 градусов и он равен половине гипотенузы, т.е. половине AD. BC=CD=6 из параллелограмма. Диагональ BD ищем из прямоугольного треугольника ABD по теореме пифагора. BD=sqrt(144-36)=6sqrt(3). Диагонали в параллелограмме точкой пересечения делятся пополам, значит OD=3sqrt(3). Треугольник DOC - прямоугольный(доказано выше). Площадь прямоугольного треугольника равна половине произведения катетов, откуда S=OD*DC/2=3sqrt(3)*6/2=9sqrt(3). Всё. Если что, sqrt - это квадратный корень. Отъ, как то так ;)

4,4(11 оценок)

Это интересно:

Искусство-и-развлечения

24.07.2022

Как найти вдохновение для написания песен?...

Здоровье

06.03.2021

Секрет понижения веса: как потерять килограмм в неделю...

Образование-и-коммуникации

19.07.2021

Как преобразовать время из 12-часового в 24-часовой формат...

Стиль-и-уход-за-собой