ответ: два решения (одно для остроугольного треугольника, другое для тупоугольного...)
1) Р = 256 (см)
2) Р = 56V21 (см)
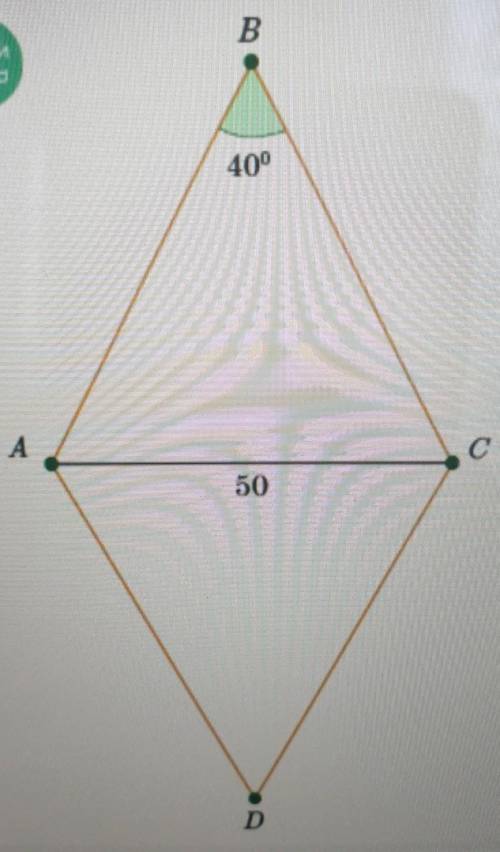
Объяснение: треугольник АВС, основание ВС=2а (чтобы не возиться с дробями); АВ=АС=b
P = 2a+2b = 2(a+b)
а=b*cos(B); по т.синусов: b=2R*sin(B)
S = 2a*h/2 = ah; h = b*sin(B)
S = P*r/2 = (a+b)*r
(a+b)*r = ab*sin(B)
b(1+cos(B))*r = b*b*sin(B)*cos(B)
(1+cos(B))*r = 2R*sin^2(B)*cos(B)
r/(2R) = (1-cos(B))*cos(B)
обозначим х=cos(B)
x^2 - x + (6/25) = 0
(5x)^2 - 5*(5x) + 6 = 0
по т.Виета корни (3) и (2)
5х=3 ---> х = 0.6
---> sin(B) = V(1-0.36) = 0.8 или
5х=2 ---> х = 0.4
---> sin(B) = V(1-0.16) = 0.2V21
b = 2*50*0.8 = 80 или
b = 2*50*0.2V21 = 20V21
a = 80*0.6 = 48 или
а = 20V21*0.4 = 8V21
P = 2*(80+48) = 128*2 = 256 или
Р = 2*(20+8)*V21 = 56V21
если опустить высоты из концов вехнего основания на нижнее и обозначить отсекаемые куски нижного отснования (от конца основания до ближайшего основания высоты) за x и y, то есть 2 уравнения.
x+y = 18-10 = 8;
17^2 - y^2 = 15^2 - x^2;
Я намеренно не буду решать это очень простую систему, а просто замечу, что 8, 15 и 17 - пифагоровы числа, то есть фигура с такими сторонами - прямоугольный треугольник. Поэтому x = 0 (ну решите системку сами, увидите:)). Итак, высота равна 15 :)));
Осталось понять, что проведенная через точку пересячения диагоналей высота делится точкой пересечения в отношении 18/10, то есть 9/5 (как основания, следует из подобия треугольников, образованных диагоналями и основаниями), поэтому длинна искомого отрезка равна
15*9/(9+5) = ну очень сложный ответ 135/14
второй 15*5/14 =75/14
Странно, кривой какой-то ответ, хотя 135+75=210, как и должно быть
может надо разделить 50 на 2 и 40 тоже на 2 потом ответы прибавляем друг другу и ответ умножаем на 2 я хз точно не могу сказать я в 5 классе