
Объяснение:
АВ=СD, по условию
AC=BD, по условию
BC-общая сторона.
∆АВС=∆DCB, по третьему признаку.
В равных треугольниках соответственные углы равны.
<АСВ=<DBC
<ABD=<DCA.
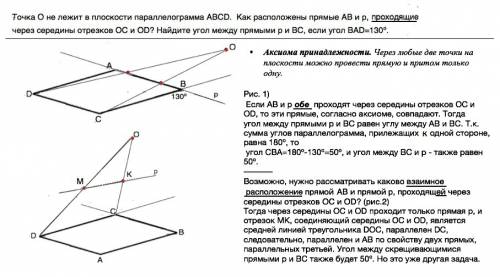
Точка О не лежит в плоскости параллелограмма ABCD. Как расположены прямые AB и p, проходящие через середины отрезков OC и OD? Найдите угол между прямыми p и BC, если угол BAD=130º
––––––––––––
Аксиома . Через любые две точки на плоскости можно провести прямую и притом только одну.. Если АВ и р обе проходят через середины отрезков ОС и ОD, то эти прямые, согласно аксиоме, совпадают. Тогда угол между прямыми р и ВС равен углу между АВ и ВС. Т.к. сумма углов параллелограмма, прилежащих одной стороне, равна 180º угол СВА=180º-130º=50º
–––––––
Возможно, нужно рассматривать каково взаимное расположение прямой AB и прямой p, проходящей через середины отрезков OC и OD, но расположенной в другой плоскости?
Тогда через середины ОС и ОD проходит только прямая р, и отрезок МК, соединяющий середины ОС и ОD, является средней линией треугольника DОC, параллелен DC, следовательно, параллелен и АВ по свойству двух прямых, параллельных третьей. Угол между скрещивающимися прямыми р и ВС также будет 50º. Но это уже другая задача.
АВ= СД - по условию
АС=ВД - по условию
ВС - общая
Следовательно, тр-к АВС = тр-ку ВСД - по 3-му признаку равенства тр-ков
Значит , < АСВ = < ДВС
и < АВД=< ДСА
Что и требовалось доказать .