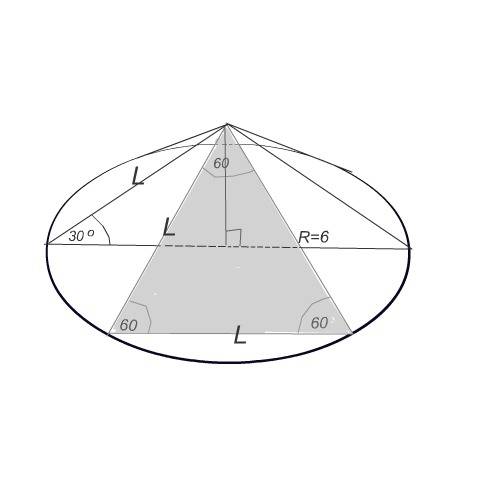
Образующая конуса наклонена к плоскости основания под углом 30°.
Плоскость сечения образована сторонами, равными образующей, и угол между ними 60°
Плоскость сечения - правильный треугольник.
Треугольник, образованный образующей, радиусом конуса и его высотой - половина правильного треугольника.
Высота - катет этого треугольника и равна половине образующей.
Второй катет равен радиусу основания и, как высота правильного треугольника
( можно и по теореме ПИфагора найти), равен (а√3):2=(L√3):2
(L√3):2=6
L√3=12 см
L=12:√3=12√3:√3*√3=12√3:3=4√3 см
Как уже сказано, плоскость сечения - равносторонний треугольник.
Формула площади равностороннего треугольника
S=(a²√3):4
S=(L√3)²√3:4=S=(16 *3)√3:4=48√3:4
S= 12√3 cм²
В окружность вписан квадрат со стороной 9 корней из 2 см. Найдите сторону правильного треугольника, описанного около этой окружности.
ответ:18√3 (см)
Объяснение:
Диаметром окружности, описанной около квадрата, является его диагональ. Точкой пересечения диагоналей квадрат делится на 4 равнобедренных прямоугольных треугольника, гипотенузы которых - стороны квадрата, а острые углы 45°. => r=9√2•sin45°=9
Центры окружностей, вписанных и описанных около правильного треугольника, совпадают ( это точка пересечения биссектрис, которые в то же время являются его срединными перпендикулярами).
Радиус вписанной в правильный треугольник окружности находят по формуле r=a:2√3 , где а - сторона правильного треугольника. =>
a=r•2√3
a=9•2√3=18√3 (см)
АС = 9 мм
Объяснение:
1) Из условия задачи следует, что ВМ = МС = ВС : 2 = 14 : 2 = 7 мм
2) Периметр ΔАВМ равен:
АВ + ВМ + АМ = 14 + 7 + АМ = 21 + АМ
3) Периметр ΔАМС равен:
МС + АМ + АС = 7 + АМ + АС
4) Так как периметр ΔАВМ больше периметра ΔАМС на 5 мм, то можно составить следующее уравнение:
РΔАВМ - РΔАМС =5
21 + АМ - (7 + АМ + АС)= 5
21 + АМ - 7 - АМ - АС = 5
21 - 7 - 5 = АС
АС = 21 - 12 = 9 мм
ответ: АС = 9 мм