Пусть х см ширина, тогда 3х см длина.
Площадь прямоугольника равна произведению дины на ширину. Составим уравнение.
х*3х=36
3х^2=36
x^2=12
x=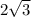
, то есть 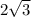см ширина прямоугольника
x=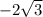
, не подходит по условию .
Тогда длина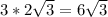 
ответ: ,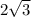 
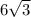
Обозначим треугольник АВС, угол С = 90 град., АС = 8 см, ВС = 6 см. Меньшая высота в треугольнике проведена к большей стороне. Самая большая сторона в прямоугольном треугольнике является гипотенузой. Найдем ее по теореме Пифагора. АВ = V(АС^2 + ВС^2) = V(8^2 + 6^2) = V(100) = 10 см. Из угла С проведем к гипотенузе высоту СD. Рассмотрим два треугольника : АВС и АDС. Они являются подобными, так как угол А у них общий и оба они прямоугольные. Из подобия запишем : ВС/АВ = СD/АС Отсюда СD = ВС*АС/АВ = 6*8/10 = 4,8 см.
Рассмотрим прямоугольный треугольник АВС, где угол А прямой. Вписанная окружность касается катета АВ в точке М, где АМ=2, МВ=8. Точка касания окружности со стороной АС точка Р, центр окружности точка О. Линии проведенные к точкам касания из цетра вписанной окружности перпендикулярны сторонам и являютс радиусами. Тогда тогда АМОР является квадратом и стороны равны 2. АМ=АР как касательные к окружности, проведенные из одной точки. Рассмотрим треугольник ВМО. у него угол М прямой, МВ и МО являются катетами. Отношение МО к МВ равно тангенсу угла МВО (tg альфа).Значит тангенс МВО=2/8=1/4. Так как центр вписанной окружности лежит на пересечением биссектрис, то ВО является биссектрисой угла АВС и равен 2МВО. Найдем тагенс АВС по формуле двойного угла. он равен 2tg альфа деленное на
1-tg^2 альфа. Подставив значения получаем 8/15. A в треугольнике АВС катет АВ=2+8=10, tg АВС=8/15, найдем катет АС=АВ*tgАВС=10*8/15=80/15=16/3=5 1/3, а гипотенузу находим по теореме Пифагора.ВС^2=10^2+(16/3)^2=1156/9
ВС=34/3=11 1/3 Получаем АВ=10, АС=5 1/3, а ВС=11 1/3
сторона1=а
сторона2=3а
а х 3а =36
3а в квадрате =36
а = 2 х корень3 = сторона1
сторона2 = 3 х 2х корень3=6 х корень3