ответ: ∠ВАС = ∠ВСА = 30 ° ; ∠АВС = 120° .
Условия задачи:
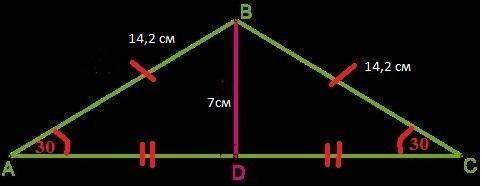
Δ АВС - равнобедренный , следовательно:
Боковые стороны равны ⇒ АВ=ВС = 14,2 см
Углы при основании равны :
АС - основание ⇒ ∠BAC (∠BAD) = ∠BCA (∠BCD)
BD =7,1 см - высота к основанию АС ⇒ является медианой и биссектрисой :
∠BDA = ∠BDC = 90° ( т.к. BD - высота)
AD = DC = АС/2 (т. к. BD - медиана)
∠ABD = ∠CBD (т. к. BD - биссектриса)
ΔBDA = ΔBDC - прямоугольные треугольники
Решение.
1) ΔBAD
По условию катет BD = 7,1 см , гипотенуза АВ = 14,2 см , следовательно :
BD = 1/2 * AB = 1/2 * 14,2 = 7,1 см
Если катет равен половине гипотенузы, то угол лежащий против этого катета равен 30° ⇒∠DAB (∠ BAC) = 30°
Проверим по определению синуса:
sin A = 7/14 = 1/2 ⇒ ∠BAC (∠BAD ) = ∠BCA (∠BCD) = 30°
2) ΔАВС :
Сумма углов любого треугольника = 180°
∠АВС = 180° - (∠ВАС + ∠ВСА)
∠АВС = 180 - 2*30 = 120 °
3.
Cумма смежных углов 180 градусов.
Если один угол 120°, то второй 180°-120°=60°
Если один угол 110°, то второй 180°-110°=70°
Сумма углов треугольника АВС равна 180 градусов, два угла 60° и 70°, значит угол А равен 180°-60°-70°=50°
4.
Сумма острых углов прямоугольного треугольника равна 90°
Если один угол 30°, то второй 90°-30°=60°
8. Треугольник равнобедренный (АВ=ВС), значит углы при основании равны
Сумма углов треугольника равна 180°
180°-50°=130° - приходится на два угла при основании
130°:2=65°
9.
Cумма смежных углов 180 градусов.
Если один угол 125°, то второй 180°-125°=55°
Треугольник равнобедренный (АВ=ВС), значит углы при основании равны.
∠А=∠С=55°
Сумма углов треугольника равна 180°
180°-55°-55°=70° - третий угол треугольника