
CH = 3√2
AB = √2
угол BAC = 45
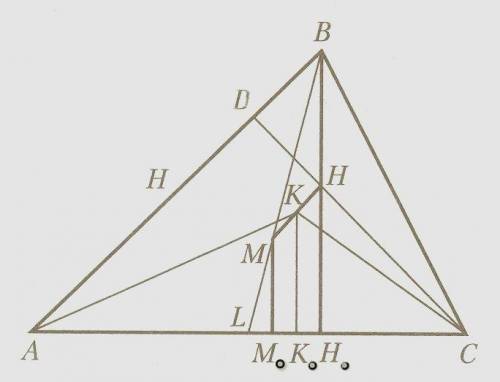
CD - высота, BL - медиана
Из точек M, K, H опустим перпендикуляры на сторону AC
В треугольнике ADC: угол ADC = 90⁰, угол DAC = угол DCA = 45⁰ (следует из условия угол BAC=45⁰)
В треугольнике HH₀C: угол HH₀C = 90⁰, угол H₀CH = угол H₀HC = 45⁰, HH₀ = CH₀ = CH*Sin45⁰ = 3
В треугольнике BH0A: AH₀ = BH₀ = AB*Sin45⁰ = 1
Трегольники BH₀L и MM₀L подобны, тогда из свойств медиан треугольника MM₀ = BH₀/3 = 1/3 (точка пересечения медиан делит их в отношении 2 к 1)
КК₀ - средняя линия трапеции MHH₀M, т.е. KK₀ = (MM₀ + HH₀)/2 = 5/3
AC = AH₀ + H₀C = 4
площадь треугольника AKC = AC*KK₀/2 = 10/3
Биссектриса правильного треугольника является и высотой и медианой этого треугольника.
Центр вписанного треугольника находится в точке пересечении биссектрис. Эта точка является и точкой пересечения медиан.
Медианы этой точкой делятся в отношении 2:1, считая от вершины .
И теперь самое интересное.
Радиус вписанной окружности в правильный треугольник равен 1/3 ее высоты ( медианы, биссектрисы)
Радиус вписанной окружности этого треугольника равен
r=24*3=8 cм
Центр описанной окружности находится в точке пересечения срединных перпендикуляров.
Срединные перпендикуляры - и высоты, и биссектрисы, и медианы.
Радиус описанной вокруг правильного треугольника окружности равен 2/3 ее высоты.
R= 24*3*2=16 cм