Дано:
ABCD-трапеция, BC и AD - основания
∠A = 90°, ∠D = 45°, BC = 4см, AB = 18см
B______C
| | \
A|______|___\ D
E
Найти:
S(ABCD) - ?
Дополнительное построение: СЕ⊥AD
∠B = ∠A = ∠C = ∠E = 90° ⇒ ABCE - прямоугольник ⇒ AB = CE = 18см,
BC = AE = 4см
Рассмотрим ΔCED:
∠D = 45°∠E = 90°CE = 18 ⇒ ∠C = 90° - ∠D = ∠D = 45° ⇒ ΔCED -р/б ⇒ ED = CE =18смAD = AE + ED = 4 + 18 = 22см
S(ABCD) =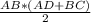 
= 
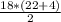= 234см²
S(ABCD) = 234см²
P.s: данные на чертёж заносить мне было проблематично, но это необходимо сделать. Мой чертёж чисто схематический, для представления фигуры создан.
1. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
2. Если две прямые, пересечённые третьей, образуют по одну сторону от третьей прямой внутренние углы, сумма которых меньше двух прямых углов, то эти две прямые пересекаются.
3:
1) если при пересечении 2-х прямых секущей накрест леж. углы равны, то прямые параллельны.
2) если при пересечении 2-х прямых секущей соответственные углы равны, то прямые параллельны.
3) если при пересечении 2- х прямых секущей сумма односторонних углов равна 180 градусов, то прямые параллельны.
4. ,то она и пересекает вторую параллельную прямую.
5. ,то соответственные углы равны.