1) Формула объёма конуса V=S•H:3=πr²H:3
Формула объёма шара
V=4πR³:3
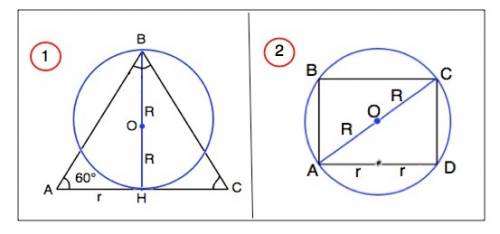
Осевое сечение данного конуса - равносторонний треугольник, т.к. его образующая составляет с плоскостью основания угол 60°.
Выразим радиус r конуса через радиус R шара.
r=2R:tg60°=2R/√3
V(кон)=π(2R/√3)²•2R²3=π8R³/9
V(шара)=4πR³/3
V(кон):V(шар)=[π8R³/9]:[4πR³/3]=(π•8R³•3/9)•4πR³=2/3
———————
2) Формула объёма цилиндра
V=πr²•H
Формула площади осевого сечения цилиндра
S=2r•H
Разделим одну формулу на другую:
(πr²•H):(2r•H)=πr/2⇒
96π:48=πr/2⇒
4π=πr
r=4
Из площади осевого сечения цилиндра:
Н=S:2r=48:8=6
На схематическом рисунке сферы с вписанным цилиндром
АВ- высота цилиндра, ВС - его диаметр,
АС - диаметр сферы.
АС=√(6²+8²)=√100=10
R=10:2=5
S(сф)=4πR8=4π•25=100π см²
1.Пусть одна сторона равна х, тогда другая 6х. У параллелограмма противолежащие стороны равны. Сумма сторон равна 84. Тогда составим уравнение
х+х+6х+6х=84
14х=84
х=84:14
х=6
Тогда 6х=6×6=36
Проверка: 6+6+36+36=84
ответ: 6; 6; 36; 36
2.В прямоугольнике противоположные стороны равны. Значит ВС=АD=18см
BD и АС являются диагоналями прямоугольника ABCD.
Диагонали в прямоугольнике равны, т.е BD=АС=22см
О-точка пересечения диагоналей, которая делит их пополам. Значит ОD=ОА=ОВ=ОС=1/2 BD=11см
Рboc=ОB+ОC+ВC
Рboc=11+11+18=40см
3.диагонали ромба являются биссектрисами его углов (то есть делят их пополам);
сумма соседних углов ромба равна 180°;
противоположные углы ромба равны
4.Диагональ АС делит параллелограмм на 2 подобных треугольника. Углы NAB=PCD, угол ABN=CDP и следовательно углы BNA= СPD, отсюда следует что прямоугольники ABN и CDP также подобны. Следовательно прямые BN и PD равны между собой. Что и требовалось доказать
5.Примем коэффициент отношения AF:FD=a. Тогда AF=a, FD=5a. Их сумма 6а=18 см, ⇒ а=18:6=3 см. Отрезок АF=3 см, отрезок FD=5•3=15 см АВСD - параллелограмм. ВС║AD, CF – секущая. ∠ВСF=∠СFD как накрестлежащие. Но ∠FCD=∠BCF (СF – биссектриса) ⇒ ∠CFD=∠FCD . Углы при основании FC треугольника FDC равны, следовательно, он равнобедренный и CD=FD=15 см ( свойство). Запомним: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Противоположные стороны параллелограмма равны, ⇒ АВ=CD=15 см. Периметр =сумма всех сторон АВСD. Р=2•(18+15)=66 см
Нужны циркуль, линейка и карандаш:
1) Если даны длины трех сторон, то:
- чертишь по линейке одну сторону;
- из каждого из краев получившегося отрезка делаешь дуги (засечки) циркулем с радиусами, равными длинам двух других сторон тр-ка, до их пересечения - это и будет третья вершина тр-ка.
- соединяешь по линейке первые две вершины с третьей.
2) Чертишь по линейке основание.
- далее делаешь засечки из каждого из концов основания радиусом равным боковой стороне до их пересечения.
- соединяешь по линейке первые две вершины с третьей.
3) То же самое, что и в п. 2) - просто основание равно боковой стороне.