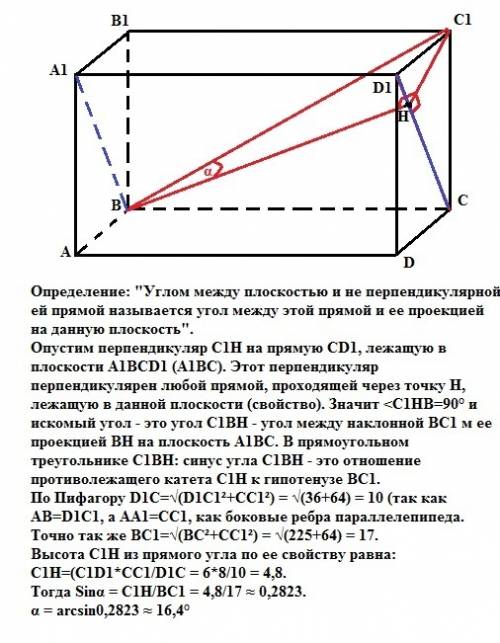
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
Суміжні та вертикальні кути, їх властивості
Суміжними називаються два кути, одна сторона яких спільна, а дві інші утворюють пряму, тобто є доповняльними променями.
Сума суміжних кутів дорівнює 180 градусам.
Два суміжних кути утворюють розгорнутий кут.
Якщо два кути рівні, то суміжні з ними кути теж рівні.
Кут, суміжний із прямим кутом, є прямим.
Кут, суміжний з гострим кутом, є тупим.
Кут, суміжний з тупим кутом, є гострим.
Будь-який промінь, що виходить із вершини розгорнутого кута і проходить між його сторонами, поділяє його на два суміжні кути.
Якщо два кути рівні, то суміжні з ними кути також рівні.
Два кути, суміжні з одним і тим же кутом, рівні.
Якщо два суміжні кути рівні, то вони прямі.
Вертикальними називаються два кути, сторони одного з яких є додатковими променями до сторін другого кута.
Вертикальні кути рівні.
При перетині двох прямих утворюються дві пари вертикальних кутів і чотири пари суміжних кутів.
Якщо відомий один із кутів, що утворились при перетині двох прямих, то знайти інші кути можна таким чином: знайти кут, суміжний з даним, враховуючи, що їх сума 180 градусів, після чого знайти кути, вертикальні з відомими, враховуючи, що вертикальні кути рівні.
Запам’ятайте поняття про теорему, аксіому та доведення.
Доведення — міркування про правильність твердження про властивість тієї або іншої геометричної фігури.
Теорема — твердження, яке треба довести.
Аксіома — твердження, що не потребують доведення, і які містяться у формулюваннях основних властивостей найпростіших фігур.