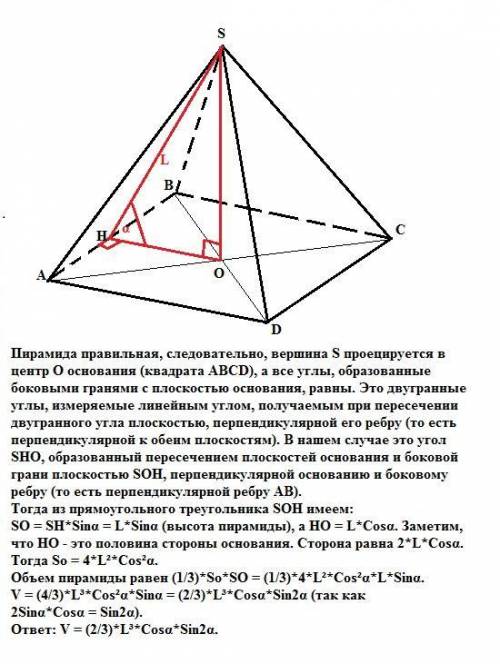
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).
Тогда из прямоугольного треугольника SOH имеем:
SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.
Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.
Тогда площадь основания So = 4*L²*Соs²α.
Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.
V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как
2Sinα*Cosα = Sin2α).
ответ: V = (2/3)*L³*Соsα*Sin2α.
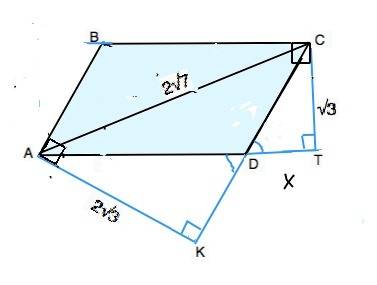
Обозначим параллелограмм АВСD. Проведем высоты из вершин острых углов параллелограмма. Они пересекутся с продолжениями сторон. СТ- высота к АD , АК - высота к СD. Прямоугольные треугольники АКD и СТD подобны по равному острому углу при D ( они вертикальные). k=AK:CT=2. Отношение площадей подобных фигур равно квадрату их коэффициента подобия. ⇒ S(AKD)=4S(CTD)
Из ∆ АСТ по т.Пифагора АТ=5. Из ∆ АСК по т.Пифагора СК=4. Площадь половины параллелограмма S(АСD)=S(ACT)-S(CTD). Она же равна S(ACK)-S(AKD) Подставим в уравнения известные значения и приравняем их. 0,5•5•√3 - S(CTD)=0,5•4•2√3 -4S(СТD), откуда получим S(CTD)=(3√3):6=0,5√3
Ѕ АВСD=2•S(ACD)=2•[(0,5•5•√3-0,5√3)]=4√3 ⇒ S²=(4√3)²=48
Пусть АВ=АС=а, ВМ=СМ=в, АМ=с.
Тогда периметр ΔАВС=АВ+ВС+АС=2а+2в=2(а+в)=32
тогда а+в=16 (см) [1]
Периметр ΔАВМ равен АВ+ВМ+АМ=а+в+с=24 (см) [2]
Отнимаем от уравнения (2) уравнение (1):
а+в+с-а-в=24-16
с=8(см)
с=АМ - искомая высота
ответ: 8 см.