ВС = 3√21 см.
Объяснение:
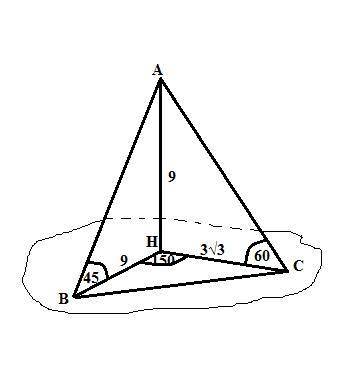
Пусть основание перпендикуляра, опущенного на плоскость α - точка Н.
AH=9 см,<ABH=45°,<ACH=60°,<BHC=150°.
Заметим, что Cos150° = Cos(180 - 30) = -Cos30° = - √3/2.
В прямоугольном треугольнике АВН острые углы равны по 45°, треугольник равнобедренный и ВН=АН= 9см.
В прямоугольном треугольнике АСН тангенс угла С равен
Tg60 = √3 = AH/CH => CH = 9/√3 = 3√3 см.
В треугольнике ВНС по теореме косинусов:
BC²=BH²+CH²-2*BН*CH*cos150 = 81+27 - 2*9*3√3*(-√3/2) или
ВС² = 108+81 =189
BC = √189 = 3√21 см.
Объяснение:
1)в<с отнимем от обеих частей неравенства 7,9
в−7,9<c−7,9 - неравенство ВЕРНО.
2)в<с умножим обе части неравенства на -7,9 (знак повернётся)
−7,9в>−7,9c - неравенство ВЕРНО.
3)в<c умножим обе части неравенства на 7,9
7,9в<7,9c - неравенство ВЕРНО.
4)в<c умножим обе части неравенства на -1 (знак повернётся)
-в>-с прибавим к обеим частям неравенства 7,9
7,9-в>7,9-с - неравенство НЕВЕРНО.
5)в<c прибавим к обеим частям неравенства 7,9
в+7,9<c+7,9 - неравенство ВЕРНО.
Если Вы учитесь в 6 классе, думаю, достаточно будет ответов "верно-неверно", а если в 9 классе, то опишите каждый шаг.
Відповідь:
якщо рівнодіюча всіх сил, прикладених до точки, дорівнює нулю
Пояснення: