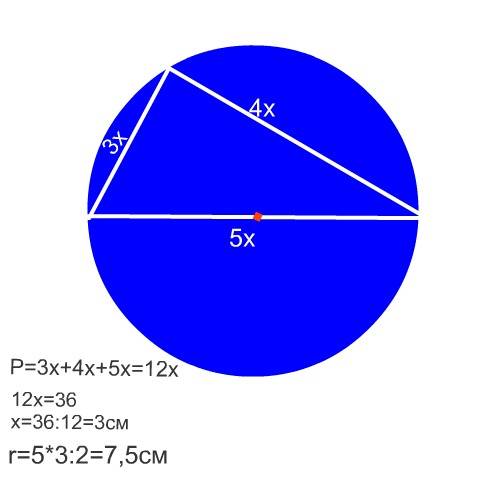
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
Исследуйте, может ли диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов.
Объяснение:
1)Все грани прямоугольного параллелепипеда - прямоугольники . ΔАВ1D - прямоугольный по т. о трех перпендикулярах : т.к. проекция ВА⊥АD , прямой лежащей в плоскости, то и наклонная АВ1⊥АD, прямой лежащей в плоскости АD⇒∠В1АD=90° .
ΔВ1СD - прямоугольный аналогично.
2) Пусть ∠AB1D=45° ,∠CB1D=60° .
В ΔAB1D , ∠ADB1=45°⇒ равнобедренный и AD=FD1=a. Тогда В1D=√(а²+а²)=а√2.
3)ΔB1CD ,cos 60°=B1C/B1D , B1C=a√2/2.
4) ΔABB1 по т Пифагора h=BB1=√(a²-b²)⇒a>b .
5 )ΔB1CC1 -прямоугольный . по т. Пифагора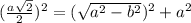 ,
,
Значит диагональ прямоугольного параллелепипеда составлять с плоскостями двух его смежных боковых граней углы 45 градусов и 60 градусов не может.