Параллелограмм - это четырехугольник, у которого противолежащие стороны попарно параллельны.
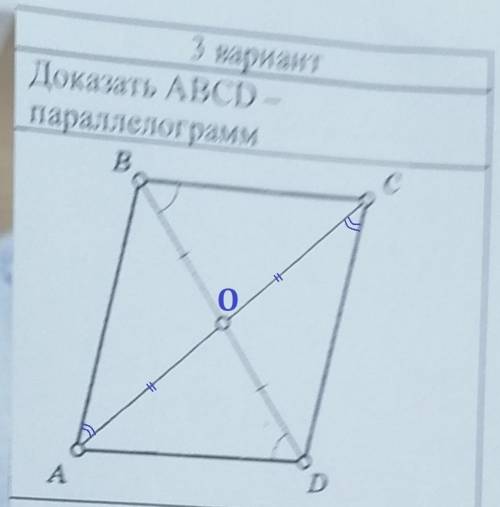
Если мы докажем, что BC║AD и AB║CD, то докажем, что ABCD параллелограмм.
1) ∠DBC = ∠BDA по условию, а это внутренние накрест лежащие углы при прямых BC и AD и секущей BD ⇒ BC║AD. (если внутренние накрест лежащие угли при двух прямых и секущей равны, то эти прямые параллельны).
2) ΔBOC = ΔAOD по второму признаку (стороне и двум углам):
BO = OD по условию, ∠OBC = ∠ODA по условию, ∠BOC = ∠AOD вертикальные углы.
В равных треугольниках соответствующие стороны равны. AO = OC
3) ΔAOB = ΔCOD по первому признаку:
BO = OD по условию, AO = OC по доказанному, ∠AOB = ∠COD - вертикальные углы.
Из равенства треугольников следует равенство соответствующих углов.
∠BAO = ∠DCO, это внутренние накрест лежащие углы при прямых AB и CD и секущей AC. ⇒ AB ║CD
4) В четырехугольнике ABCD AD║BC и AB ║ CD. Четырехугольник ABCD параллелограмм.
Доказано.
Объяснение:
1) a) C1D
b) AB + AD + AA1 = AB + BC + CC1 = AC + CC1 = AC1
c) B1C - AD = B1C - B1C1 = C1C
d) |DC1|² = 32 + 32 = 64
|DC1| = 8
2) а) ВА + ВС + ВВ1 + D1A = BA
б) BB1 + CD + A1D1 + D1B = BB (здесь как не заменяй вектора, получается ВВ)
а) AB + CC1 + A1D1 + C1A = AA (тоже самое)
б) AB + AA1 + AD + C1D = AD
3) а) CC1 = AA1 ÷ 12см
СВ = DA = 8 см
СD = BA = 9 см
б) |DC1|² = DD1 + D1C1 = DD1 + DC = 144 + 81 = 225
|DC1| = 15 см
|DB|² = DA + AB = 81 + 64 = 145
|DB| = корень из 145
|DB1|² = AD + BB1 = AD + DD1 = 144 + 64 = 208
|DB1| = 4 корень 13
попробуй это Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.