2. S=1/2*6*8=24 см²
чтобы найти периметр,надо найти сторону. находим по теореме Пифагора:
√(1/2*6)²+(1/2*8)²=5
Р=5*4=20 см
4. При пересечении двух хорд произведение длин отрезков, образованных точкой пересечения, одной хорды, равно произведению длин отрезков другой хорды.
АМ * ВМ = СМ * ДМ.
Пусть длина отрезка СМ = Х см, тогда ДМ = (23 – Х) см.
12 * 10 = Х * (23 – Х).
120 = 23 * Х – Х2.
Х2 – 23 * Х + 120 = 0.
Решим квадратное уравнение.
Х1 = 8 см.
Х2 = 15 см.
Если СМ = 8 см, ДМ = 15 см.
Если СМ = 15 см, ДМ = 8 см.
ответ: Длины отрезков равны 8 и 15 см
5. если в окружность вписан прямоугольный треугольник, то его гипотенуза-это диагональ этой окружности, внашем случае она равна 6,5*2=13. по теореме пифагора найдем неизветсный катет, он равен:
корень из гипотенуза квадрате минус другой катет в квадрате, это равно 13*13-5*5=12
площадь треугольника это половина произведения катетов, то есть 0,5*5*12=30
ответ: 30
Объяснение:
1 фото - 1 номер
2 фото - 3 номер
1. 4 см.
2. 84 см.
3. 2√26 см.
Объяснение:
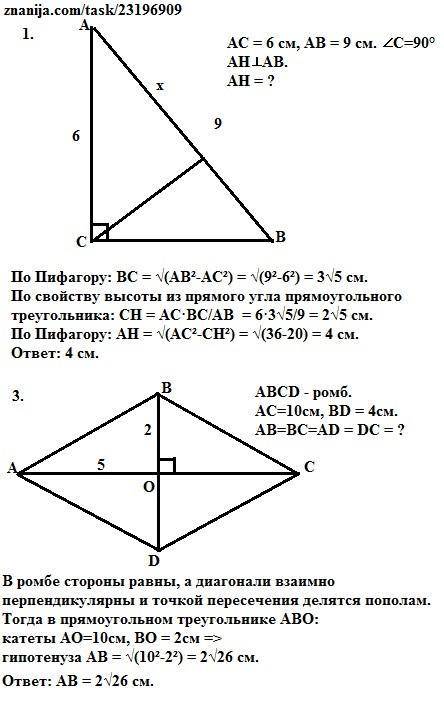
1. По Пифагору: ВС = √(АВ²-АС²) = √(9²-6²) = 3√5 см.
По свойству высоты из прямого угла прямоугольного треугольника:
СН = АС·ВС/АВ = 6·3√5/9 = 2√5 см.
По Пифагору: АН = √(АС²-СН²) = √(36-20) = 4 см.
ответ: 4 см.
2. По Пифагору второй катет равен √(37²-35²) = √(2·72) = 12см. Тогда периметр треугольника (сумма его трех сторон) равен:
37+35+12 = 84см.
ответ: 84см.
3. В ромбе стороны равны, а диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.
Тогда в прямоугольном треугольнике АВО:
катеты АО=10см, ВО = 2см =>
гипотенуза АВ = √(10²-2²) = 2√26 см.
ответ: 2√26 см.
r=(a+b-c)/2
2=(a+b-10)/2
a+b-10=4
a+b=14 (1)
(a+b)^2=196
По формуле квадрата суммы (а+b)^2=a^2+2ab+b^2=(a^2+b^2)+2ab
Т.к. гипотенуза 10см, a^2+b^2=10^2=100. Подставляем в формулу квадрата суммы:
100+2ab=196
2ab=96
ab=48 (2)
Выражаем из (1), например, а
a=14-b
Подставляем в (2):
(14-b)b=48
14b-b^2=48
b^2-14b+48=0
Решаем квадратное уравнение
b=-(-14/2)+/-квадр. корень из (14/2)^2-48
b=7+/-1
Катеты равны 6см и 8см
Площадь треуг.=6*8/2=24кв.см