
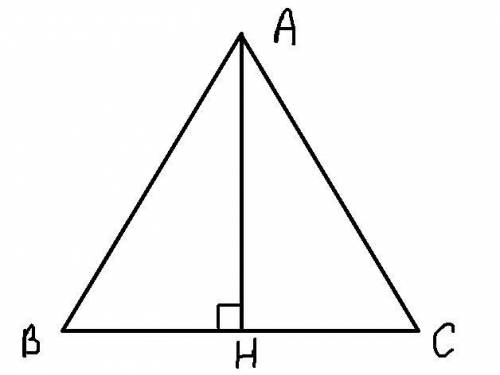
(Смотри вложение)
S = 0,5 * BC * AH
Т.к. ΔABС - равносторонний ⇒ AH является не только высотой, но и биссектрисой и медианой. Из этого можно сделать вывод, что ∠BAH = ∠CAH = 30° и BH=СН
Рассмотрим ΔABH
ΔABH - прямоугольный, т.к. AH -высота
Пусть х - BH, тогда 2х - ВА (т.к. треугольник ΔABС равносторонний и сторона, лежащая напротив ∠ 30° равна половине гипотенузы), тогда по т. Пифагора:
х² + (12√3)² = (2х)²
х² - 4х² + 432 = 0
-3х² = - 432 | : (-3)
х² = 144
x = 12 ( корень -12 мы не берём, т.к. сторона треугольника не может быть отрицательной)
Получается ВС = 2 * ВН = 2*12 = 24
S = 0,5 * 24 * 12√3 = 12 * 12√3 = 144√3 см²
ответ: S = 144√3 см²
0,08√2м
Объяснение:
√16=4см сторона одной клетки.
FD=4*4=16см
SK=3*4=12см
FK=1*4=4см
КD=3*4=12см
KD=SK.
∆SKD- прямоугольный треугольник.
По теореме Пифагора найдем гипотенузу
SD=√(SK²+KD²)=√(12²+12²)=12√2см.
S∆FSD=1/2*SK*FD=1/2*12*16=192/2=96см²
S∆FSD=1/2*FP*SD,
FP=2*S∆FSD/SD=2*96/12√2=192/12√2=
=16/√2=8√2√2/√2=8√2см
1м=100см
8√2/100=0,08√2м