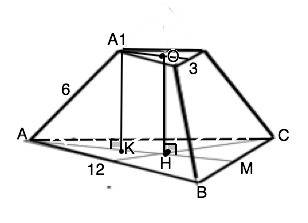
Центры оснований О и Н - центры описанных около них окружностей, т.к. являются точками пересечения срединных перпендикуляров.
Радиус описанной окружности правильного треугольника R=a/√3 ⇒
А1О=3:√3=√3 дм
AH=12:√3=4√3 дм
Опустим из вершины А1 перпендикуляр А1К на нижнее основание. А1К=ОН ( высоте пирамиды, т.к. расстояние между параллельными плоскостями одинаково в любой точке).
АК=АН-А1О=4√3-√3=3√3
По т.Пифагора
A1К=√(АА1²-АК²)=√(36-27)=3.
Высота ОН=А1К=3
КМ ║ТР║ АС⇒ соответственные углы, образованные при их пересечении секущей АВ, равны, а угол В для всех трех треугольников общий.
∆ АВС ~ ∆ТВР~∆ КВМ по двум углам, прилежащим к одной стороне.
АВ=3 части, ТВ=2 части. КР=1 часть.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
АВ:ТВ=3:2=k₁
S ∆ ABC:S ∆ TBP=k₁²=9/4
AB:KB=3:1=k₂
S ∆ ABC:S ∆ KBM=k₂²=9/1
TB:KB=2:1=k₃
S ∆ ТВР: S∆ КВМ=k₃²=4/1