1); 2).
Объяснение:1) Верно.
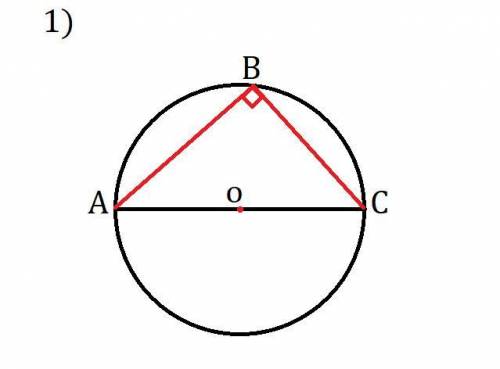
Следствие: "Вписанный угол, опирающийся на полуокружность (или на диаметр), - прямой".
Смотрим: ∠ABC опирается на диаметр (или на полуокружность). Значит, ∠ABC - прямой.
В полуокружности всего 180°.
Теорема: Вписанный угол измеряется половиной дуги, на которую он опирается.
Смотрим: на рисунке "1)" ∠ABC опирается на полуокружность или на дугу AC, которая равна 180°. Если дуга дуга равна 180°, то по теореме о вписанном угле, ∠ABC = 180˚/2 = 90˚.
2) Верно.
Теорема: "Сумма двух сторон треугольника должна быть больше третьей стороны".
Смотрим: 1 + 2 = 3; 3 < 4.
Поэтому такого треугольника не существует.
3) Неверно.
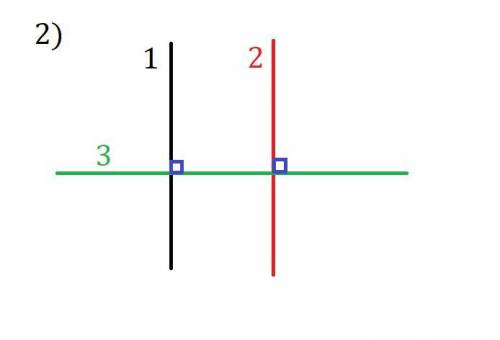
На рисунке "2)" прямые 1 и 2 перпендикулярны к прямой 3.
Поэтому прямые 1 и 2 параллельны, а не перпендикулярны.
треугольник АВС, АВ=6, АС=8, площадь АВС=12*корень2=1/2*АВ*АС*sinA, 24*корень2=6*8*sinA, sinA=24*корень2/48=корень2/2 - что соответствует углу 135 , ВС в квадрате=АВ в квадрате+АС в квадрате-2*АВ*АС*cos135=36+64-2*6*8*(-корень2/2)=100+48*корень2, ВС=корень(100+48*корень2), = 12,96