Объяснение:
3. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-7°=83° .
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=83°.
4. 1) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания,
значит ∠ ОКМ=90°-84°=6°
2) ∆ ОКМ- равнобедренный (ОК=КМ=r) , значит ∠ОКМ=∠ОМK=6°.
5. ∠ ABC =90°(вписанный), т.к ∪ АС=180° (опирается на диаметр АС). Тогда ∠С=180°-90°-75°=25°
6. 1) ∪ AN=73°·2=146° (стягивает вписанный ∠ NBA). Тогда
∪ NB =∪ AB-∪AN=180°-146°=34°.
2) ∠NMB=34°/2=17° (вписанный не центральный угол)
7. 1) ∆ АОВ- равнобедренный(АО=ОВ=r), значит ∠ОАВ=∠АВО=15°. Тогда ∠ОВС =56°-15°=41°.
2) ∆ ВОС- равнобедренный(ВО=ОС=r), значит ∠ОВС=∠ВСО=41°.
8. ∆ АОВ =∆ СОD (AO=OD=r, CO=OB=r, ∠AОВ =∠CОD-вертикальные ), значит ∠ОАВ =∠ОСD=25°
...
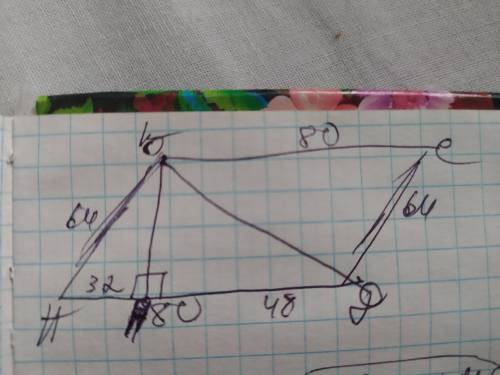
ответ: ВД приблизительно 73,32см
Объяснение: так как нам известно, что сторону АД =80 ° делит высота ВН, отсекая от неё отрезок 32см, то второй отрезок будет: 80-32=48см;
АН=32см; НД=48см. Рассмотрим ∆АВН- он прямоугольный и ,зная в нём две стороны, найдём по теореме Пифагора высоту ВН:
ВН²=64²-32²=4096-1034=3072=√3072
ВН=√3072см. Теперь рассмотрим ∆ВДН - он тоже прямоугольный и, зная высоту ВН мы можем найти диагональ ВД- расстояние между вершинами тупых углов по теореме Пифагора:
ВД²=48²+3072= 2304 +3072=5376
ВД=√5376=√256×√21=16√21(см). Если округлить до сотых будет приблизительно 73,32(см)
29°; 87°; 64°.
Объяснение:
Пусть х - первый угол, тогда 3х - второй угол, а (х+35°) - третий угол.
Так как сумма внутренних углов треугольника равна 180°, то:
х + 3х + (х+35°) = 180°
5х + 35 = 180
5х = 180 - 35
5х = 145
х = 145 : 5 = 29° - первый угол;
3х = 3 · 29 = 87° - второй угол;
х+35 = 29+35 = 64° - третий угол треугольника.
Проверка:
29 + 87 + 64 = 180°.
ответ: 29°; 87°; 64°.