Решенье во вложеньях Уе-ха!
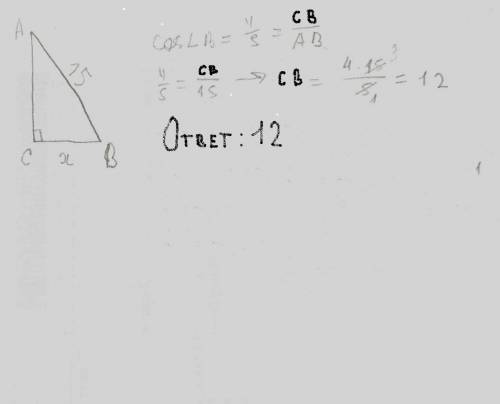
Объяснение: №1. а₃=6√3, ⇒ r = а₃/2√√3 = 6√3 /2√√3= 3, a₆=r=3, ⇒ P₆=3·6=16, S₃ = a₃²√3/4 = 108√√3/4 = 28√3 №2. a₄ = 5√3, но а₄ =R√2, ⇒ R= 5√3/√2 = 5√6/4; ⇒А₄=2Rtg45°=2R = 5√6/2; ⇒ p₄= 4·5√3= 20√√3, P₄= 4·5√6/2 = 10√6; s₄= (5√3)²= 75, S₄= (5√6/2)²=37,5 №3. a₃= 3√5, ⇒ R = a₃/√3= 3√5/√3 = √15; a₆= 2Rtg(180°/6) = 2√15· √3/3= 2√√5; P₆= 6·2√5 =12√5; S₃= а₃²√3/4 = (3√5)²·√3/4 = 45√3/4
Обозначим трапецию АВСD, AB=CD, АD=12√3, ∠BAD=60°. ∠ABD=90°. Треугольник АВD- прямоугольный, ⇒ ∠АDB=180°-90°-60°=30°. Сторона АВ противолежит углу 30° и равна половине AD. АВ=6√3. Опустим высоту ВН на большее основание. Треугольник АВН - прямоугольный, ∠АВН=180°-90°-60°=30°. Катет АН=АВ:2=3√3. ⇒ DH=AD-AH=12√3-3√3=9√3. Высота ВН=АВ•sin60°=6√3•(√3/2)=9. Высота равнобедренной трапеции, проведенная из тупого угла, дели основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности⇒ DH=(AD+BC):2. Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=BH•DH=9•9√3=81√3 (ед. площади)
косинус это прилежащая сторона делёная на гипотинузу,значит можно составить пропорцию 4/5=ВС/ВА,подставляем цифры 4/5=ВС/15 решаем пропорцию 4*15=5ВС отсюда 60=5 ВС получаем 12=ВС ответ:ВС равно 12