Только потому, что налажал в комментариях.
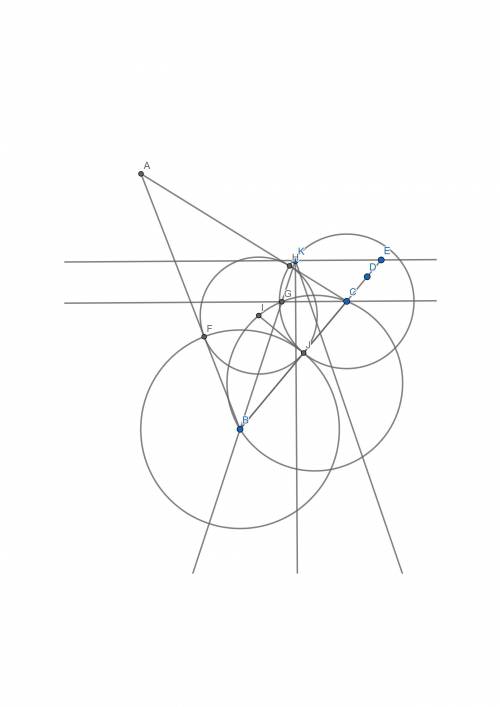
См. чертеж.
1) строится заданный угол φ, на чертеже это угол с вершиной в точке K. Проводится биссектриса и перпендикулярная ей прямая KE. Строится в общем произвольный отрезок BE, концы которого расположены как на чертеже.
Смысл в том, что из точки K отрезок BE виден под углом 90° + φ/2.
2) на отрезке BE от точки B откладывается заданная сторона a, получается точка C. Проводится CG II KE.
Теперь заданная сторона BC = a видна из точки G под углом 90° + φ/2.
3) строится описанная окружность треугольника BCG.
Эта процедура всем известна, я её на чертеже не отображаю, тем более, что GeoGebra строит её автоматически.
4) от точки C во вне отрезка BC откладывается заданная разность d, получается точка D, то есть CD = d. Отрезок BD делится пополам, так находится точка J (то есть BJ = JD).
5) из точки J проводится перпендикуляр к BC до пересечения с окружностью (BGC) в точке I.
I - центр вписанной окружности искомого треугольника
6) проводится окружность с центром I и радиусом IJ.
вписанная окружность.
7) проводятся две окружности - с центром B и радиусом BJ и центром в C и радиусом CJ. Так находятся точки пересечения этих окружностей с вписанной окружностью - точки F и H.
Они же - точки касания боковых сторон.
8) проводятся BF и CH до пересечения в точке A.
ABC - искомый треугольник.
Даны : А(2,1,0), М(3,-2,1), N(2,-3,0).
Находим координаты направляющего вектора прямой NM:
NM: (1; 1; 1).
Принимаем координаты направляющего вектора прямой NM как соответствующие координаты нормального вектора n плоскости α :
n = (A; B; C). То есть, A = 1, B = 1, C = 1.
Записываем уравнение плоскости, проходящей через точку А(2; 1; 0) и имеющей нормальный вектор n(A; B; C), в виде:
A(x -x1) + B(y - y1) + C(z - x1) - это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Подставляем данные -
α: 1(x -2) + 1(y - 1) + 1z = x + y + z - 3 = 0.
ответ: уравнение плоскости α: x + y + z - 3 = 0.