Можно доказывать по разному либо через стороны либо через диогонали
Думаю через диогонали будет быстрее
Своиство деогоналей ромба таково диогонали ромба перпендикулярны друг другу и точкой пересечения делятся пополам
по этому нам нужно просто нпити их длину
ну а про стороны магу сказать что все стороны ромба ровны можно наити их и это тоже может послужить докозательством

2√3 ед.
Объяснение:
Во условию в ΔABC AB=5 ед., AC=7 ед. , BC =10 ед.
Медиана АО - медиана, проведенная к большей стороне BC.
Достроим ΔABC до параллелограмма ABDC.
Диагонали параллелограмма пересекаясь, точкой пересечения делятся пополам , тогда AD= 2* AO.
По свойству квадратов диагоналей параллелограмма : сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон.
AD² +BC² = 2*( AB²+AC²);
(2AO) ²+BC² = 2*( AB²+AC²);
4AO² +BC² = 2*( AB²+AC²);
4AO² + 10²=2*( 5²+7²);
4AO² = 2*( 25+49)-100;
4AO² =48;
AO² =48:4;
AO² =12;
AO= √12=√(4*3)=2√3 ед.
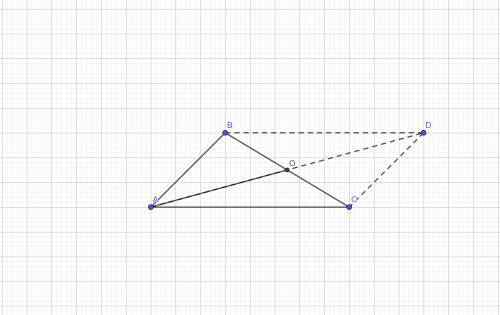
Отложим эти точки на координатной плоскости и докажем, что ABCD - ромб
Точка пересечения AC и BD == О
Из рисунка следует, что диагонали АС и BD перпендикулярны. Если такой тип решения не подходит, можно сказать, что координаты иксов точек B, D равны и координаты игриков А, С равны, => они находятся на двух перпендикулярных прямых
Треугольники ABO, BOC, COD, DOA равны по двум катетам, => их гипотенузы тоже равны.
Следовательно, ABCD - ромб, т.к. все его стороны равны, а диагонали перпендикулярны