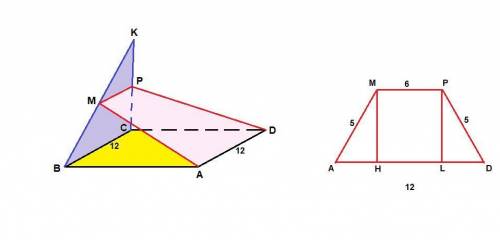
1) MPDA - равнобедренная трапеция
2) 36 см²
Объяснение:
1) МР - средняя линия треугольника ВСК, поэтому
МР║ВС и МР = 1/2 ВС = 6 см
МР║ВС, ВС║AD, ⇒ МР║AD.
Значит, MPDA трапеция. А так как МА = PD = 5 см, то
MPDA - равнобедренная трапеция.
2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда
HL = MP = 6 см.
ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит
АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см
ΔАМН: прямоугольный, египетский, значит МН = 4 см.
Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²
Высота пирамиды H = bsinβ.
Проекция ребра равна bcosβ, а проекция апофемы (bcosβ) / 2.
По Пифагору находим апофему А = √((b²cos²β/4)+b²sin²β) =
=(b/2)√(cos²β+4sin²β).
2) Угол при вершине треугольника α = arc cos(m/m+n).
3) a*sin α = (b/cos α) + (b/sin α). После приведения к общему знаменателю получаем a*sin²α*cos α = b(sin α+cos α).
Если заменить sin α+cos α = b√2(cos(π/4)-α) = b√2(sin(π/40+α).
Тогда получим b = (a*sin²α*cosα) / (√2sin(π/4)+α).