Пирамида усечена плоскостью, параллельной основанию.
Отсеченная пирамида подобна исходной 6:8 =3:4
Следовательно, части, заключенные между плоскостями, относятся к исходным 1:4.
Найдем высоту и апофему исходной пирамиды.
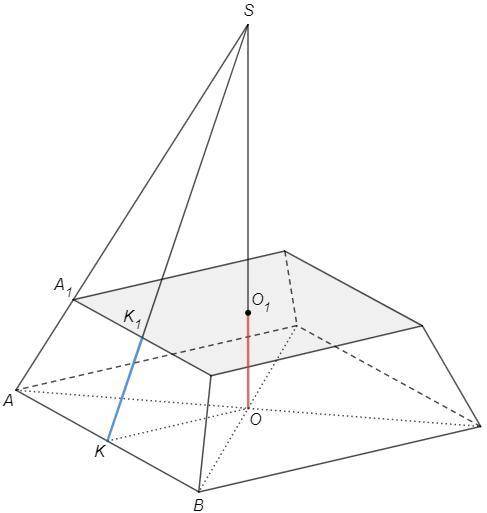
Правильная пирамида, в основании квадрат, вершина падает в центр основания.
Центр описанной окружности квадрата - пересечение диагоналей.
Диагонали квадрата перпендикулярны, равны, точкой пересечения (O) делятся пополам.
AO =AB sin45 =8*√2/2 =4√2
SO⊥(ABC), SAO=60
SO =AO tg60 =4√2*√3 =4√6 (исходная высота)
Боковые грани правильной пирамиды - равнобедренные треугольники.
Высота боковой грани - апофема - является медианой.
K - середина AB, KO=AB/2=4 (медиана из прямого угла)
SK =√(SO^2+KO^2) =4√(1+6) =4√7 (исходная апофема)
OO1/SO =KK1/SK =1/4
высота усеченной пирамиды OO1=√6 (см)
апофема усеченной пирамиды KK1=√7 (см)
Площадь трапеции находится по формуле S=4r^2/sin угла альфа, где r - радиус вписанной окружности, а угол альфа-это угол при основе тропеции, по условию он равен 45 градусов. Подстовляем
S=(4r^2)/sin 45=8 r^2/ корень из 2= 36 корень из 2.
36 корень из 2= 8 r^2/ корень из 2
72= 8r^2
r^2= 72/8=9
r=3.
А как извесно высота в трапеции ровна диаметру, значит h=2r=6