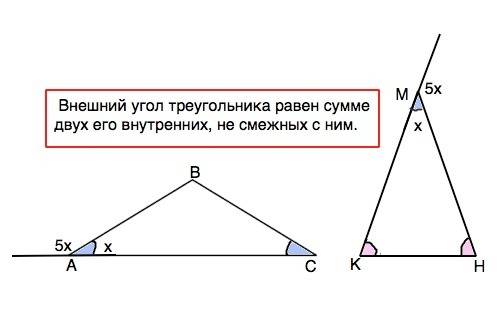
Сумма углов треугольника 180°. Внешний угол треугольника равен сумме двух других, не смежных с ним.
Примем меньший внутренний угол равным х, тогда смежный внешний равен 5х. Их сумма равна градусной величине развернутого угла.
5х+х=180°⇒
х=30°
Случай 1:
Данный равнобедренный треугольник тупоугольный, тогда два его острых угла равны по 30°, третий из суммы углов треугольника равен 180°-2•30°=120°
Случай 2:
треугольник остроугольный. Меньший угол 30°, два других по
(180°-30°):2=75°
1) 30°, 30°, 120°
2) 30°, 75°, 75°
Объяснение: Для прямоугольных треугольников должна выполняться теорема Пифагора - сумма квадратов катетов = квадрату гипотенузы. Гипотенуза в прямоугольном треугольнике самая большая сторона. Тогда имеем:
2) 11² +20² =? 25² т.е 121 + 400 = 521, 25² = 625. Прямоугольный треугольник такие стороны иметь не может, так как 521 ≠ 625
3) 18² + 24² =? 30² т.е. 324 + 576 = 900, 30² = 900. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 18² + 24² = 30² выполняется.
4) 9² + 12² =? 15², т.е. 81 + 144 = 225, 15² = 225. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 9² + 12² = 15² выполняется.
Условие задачи 1) не ясно. Решить нельзя.