S = 50 ед².
Объяснение:
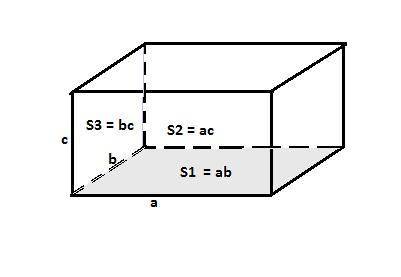
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны
a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).
Выразим сторону b из равенств (1) и (3) и приравняем полученное:
b = 48/a и b = 30/c => 48/a = 30/c => c = 30a/48 = (5/8)a.
Подставим это значение в (2):
a·(5/8)a = 40 => a² = 320/5 = 64 => a = 8 ед.
Тогда из (1) b = 48/8 = 6 ед. c = 30/8 = 5 ед. (из 2).
Найдем по Пифагору диагональ основания:
d = √(a²+b²) = √(64+36) = 10 ед.
Площадь диагонального сечения равна:
S = d·c = 10·5 = 50 ед².
ответ: 34 см
Объяснение:
1. Расстояния от концов диаметра до касательной -- это перпендикуляры к касательной из этих концов.
AB = 15 см, CD = 19 см
2. O - центр окружности, E - точка касания. Проведём OE. По свойству касательной к окружности OE ⊥ AD
3. Так как OE ⊥ AD, AB ⊥ AD, CD ⊥ AD, то AB ║ CD ║ OE
4. AB║CD ⇒ ABCD - трапеция
5. BO = OC, AB║CD║OE ⇒ AE = ED (теорема Фалеса)
6. Из пункта 5 следует, что OE - средняя линия трапеции ABCD.
OE = (AB + CD)/2 = (15+19)/2 = 34/2 = 17 см
7. OE - радиус. Тогда диаметр BC = 2OE = 2*17 = 34 см