Угол АОС и ВОС- смежные, значит, угол ВОС= 180-120= 60
Треугольник ОВС- равносторонний, поэтому все углы в нем по 60. Угол АВС=60. ч.т.д.
а) В прямоугольной системе координат уравнение сферы радиуса R с центром в точке С(Xo; Yo; Zo) имеет вид:
(x - xo)² + (y - yo)² + (z - zo)² = R².
Значит, надо выделить полные квадраты в заданном уравнении
x² + y² + z² - 4x + 6y = 36.
(x² - 4x + 4) - 4 + (y² + 6y + 9) - 9 + z² = 36.
(x - 2)² +( y + 3)² + z² = 49.
Теперь видны координаты центра сферы: О(2; -3; 0) и величина радиуса R = √49 = 7.
б) Расстояние от центра сферы до заданной плоскости x = −6 равно 2 - (-6) = 8.
Так как радиус равен 7, то сфера не касается такой плоскости.
Вступление:
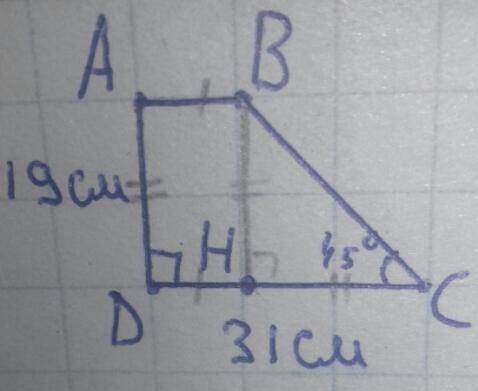
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
угол СОВ =180-120=60. треугольник ОСВ равнобедренный ОС+ОВ=радиус, угол ОСВ=уголСВО=(180-60)/2=60, треугольник равносторонний все углы по 60, угол СВО=60