Прямоугольный параллелепипед
- ребра из одной вершины взаимно перпендикулярны
- противоположные грани - равные прямоугольники
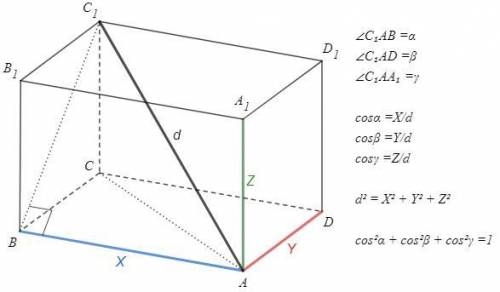
AC1=d, AB=X, AD=Y, AA1=Z
AB⊥(BBC1) => AB⊥C1B
d^2 =Z^2 + AC^2 (т Пифагора)
AC^2 =X^2 +Y^2
=> d^2 =X^2 +Y^2 +Z^2
В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех измерений.
∠C1AB =a, ∠C1AD=b, C1AA1=y
cosa =X/d, cosb =Y/d, cosy =Z/d
Возведем в квадрат и сложим:
cosa^2 +cosb^2 +cosy^2 =(X^2 +Y^2 +Z^2)/d^2 =d^2/d^2 =1
Сумма квадратов направляющих косинусов вектора равна единице.
Объяснение:
10 см. Либо по самому простому : точка пересечений делит на половину стороны квадрата, либо пойти более длинным путем и решить через прямоугольный треугольник. ABCD - квадрат; a - AD=DC=CB=AB = 20 см; AC=BD - диагональ; О - точка пересечения диагоналей; OG - высота, проведенная в треугольнике AOD. Диагональ квадрата: AC=BD = a√2 = 20√2 (см). BO=OD=AO=OC = 20√2/2 = 10√2 (cм). AG=GD = a/2 = 20/2 = 10 (см). Рассматриваем треугольник DGO. (DO - гипотенуза, DG - 10 см, GO - ?) По т. Пифагора: GO = √DO² - DG² = √(10√2)² - 10² = √100*2 - 100 = √200-100 = √100 = 10 (cм)
Треугольник АВС, АВ=ВС, АС=12, высота=медиане = ВН, АН=СН = 12/2=6
АВ=АС=а,
Периметр = а+а+12=2а+12, полупериметр=(2а+12)/2 = а+6
радиус= площадь/полупериметр
площадь = радиус х полупериметр = 3 х (а+6) = 3а+18
ВН = корень(АВ в квадрате - АН в квадрате) = корень(а в квадрате - 36)
площадь = 1/2АС х ВН = 6 х корень(а в квадрате - 36)
приравниваем площади
3а+18 = 6 х корень(а в квадрате - 36) - возводим две части в квадрат
27а в квадрате - 108а -1620=0
а = (108+- корень(11664+ 4 х 27 х 1620) ) / 2 х 27
а= (108+- 432) / 54
а = 540/54 =10 = АВ=АС
высота ВН = корень(100-36) = 8
площадь = 1/2 х 12 х 8 = 48