
68. По данным на рисунке найдите площадь 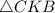 .
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :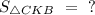 Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 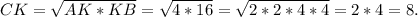
Следовательно, 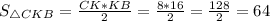 ед².
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите 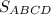 .
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :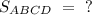
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 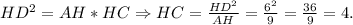
Следовательно, 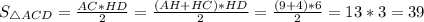 ед².
ед².
Тогда 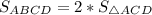 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
78 ед².
АВ-гипотенуза, АF=1/2×AВ(половине гипотенузы), значит, угол(противолежащий) В=30° или 45°( т.к. по теореме в прямоугольном треугольнике напротив этих углов лежит сторона равная половине гипотенузы).
если В=45°, значит, уголА=45°, т.к. сумма острых углов треугольника =90°,FB=4,5
следовательно,
проверка:
по теореме Пифагора:
АВ^2=АF^2+FB^2
81=20,25+FB^2
FB^2=60,75
FB=7.79422
FB≠AF
значит, угол В=30°
А=180-30=150°(сумма смежных углов ромба =180°).