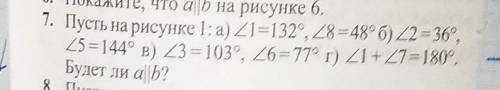
1. Периметр соевого сечения конуса равен 360 ед.
2. Объем конуса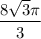 
ед.³
Объяснение:
Требуется найти:
1. Периметр соевого сечения конуса.
2. Объем конуса.
498.
Дано: Конус.
АК = 100; sin∠АКО = 0,6.
Найти: Р (КАМ)
1. Рассмотрим ΔКАО - прямоугольный.
Синус угла - отношение противолежащего катета к гипотенузе.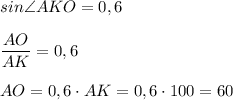
По теореме Пифагора:
КО² = АК² - АО²
КО² = 10000 - 3600 = 6400
КО = 80
⇒ КМ = 80 · 2 = 160
Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)
504.
Дано: Конус;
r = СО = 2; ∠ВСО = 60°;
Найти: V конуса.
Объем конуса найдем по формуле:
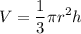, где r - радиус основания, h - высота конуса.
1. Рассмотрим ΔСВО - прямоугольный.
Тангенс угла - отношение противолежащего катета к прилежащему.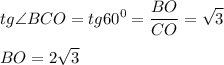
2. Найдем объем:
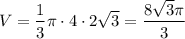(ед.³)
Рассмотрим треугольник AOC и треугольник BOD:
угол AOC равен углу BOD(как вертикальные)
AO=OB и CO=OD(по условию,т.к. точка серединой является O)
значит треугольник AOC равен треугольнику BOD(по двум сторонам и углу между ними)
значит угол DAO равен углу CBO(в равных треугольниках против равных сторон лежат равные углы)
номер 2: Рассмотрим треугольник ABD и треугольник ADC:
по условию угол BDA равен углу ADC
сторона AD-общая
и по условию угол BAD=углу DAC(т.к. AD биссектриса)
Значит треугольник ABD равен треугольнику ADC(по двум углам и стороне между ними)
значит сторона AB=AC(т.к. в равных треугольниках против равных углов лежат равны стороны)