
В задании на рисунке две прямых с.
Изменив рисунок, получаем: прямая d пересекает три прямые a, b и с.
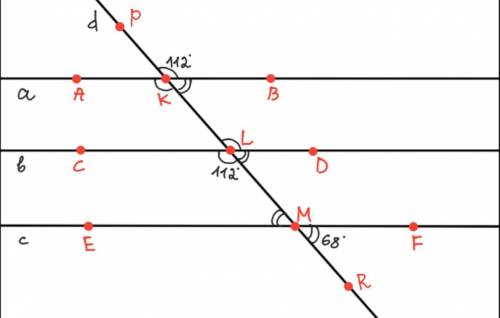
Чтобы была возможность именовать углы, обозначим на прямых точки A, B, C, D, E, F, K, L, М, Р и R (см. рисунок).
Не забываем: )
Если при пересечении двух прямых секущей накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые параллельны.
1) Вертикальные углы при пересечении двух прямых всегда равны, а это значит:
∠РКВ=∠AKL=112°,
∠KLD=∠CLM=112°,
∠EML=∠RMF=68°.
2) Как видим из предыдущего пункта, ∠PKB=∠KLD=112° ⇒ прямые a и b параллельны, т.к. углы равны как соответственные, а прямая d — секущая.
3) Прямые b и c тоже параллельны, покажем это.
Известно, что ∠CLM=122°, ∠EML= 68°.
∠CLM+∠EML=122°+68°=180°.
Согласно теореме, если две прямые при пересечении секущей параллельны, то их односторонние углы в сумме составляют 180°.
∠CLM+∠EML=180° ⇒ прямые b и c параллельны! (т.к. сумма одностор. углов 180°, прямая d — секущая)
4) Из 2 и 3 пунктов известно, a||b и b||c ⇒ a||c ⇒ a||b||c.
ответ: прямые а, b и с параллельны.
1. Здесь образуются два подобных (по трем углам) треугольника (большой и малый). Для них можно записать соотношение:
1,7/4 = х/8+4
откуда
х = 1,7/4 * 12 = 3 * 1,7 = 5,1
ответ: 5,1
2. 0,5 * 4=2 метра
3.Перерисуем данный рисунок в виде треугольников и обозначим интересующие нас точки.
Рассмотрим треугольники ABC и DCE.
Эти треугольники подобны, т.к.:
∠C - общий,
∠B и ∠DEC - прямые,
углы A и EDC - равны, так как являются соответственными.
Из подобия этих треугольников следует, что:
AB/DE=BC/EC
BC=(AB*EC)/DE=(9*1)/2=4,5.
В задаче нас интересует отрезок BE, BE=BC-EC=4,5-1=3,5.
ответ: 3,5
ответ 4) нельзя найти
Ну тока не оч поимаю поч ты написал 1 вариант выбрать