2. 5 см.
3. 8 см, 18 см.
4. 7 см.
Объяснение:
"2. Периметр трапеции равен 22см, но и боковые стороны - 4см и 8см. Найти среднюю линию трапеции.
3. Одна из основ трапеции на 10см меньше за вторую, а ее средняя линия равен 13см. Найдите основы трапеции,
4. Диагональ равнобедренной трапеции является биссектрисой острого угла. Найти боковую сторону трапеции, если основы равны 7см и 15см."
***
2. Р ABCD=AB+BC+CD+AD=22 см.
4+BC+8+AD=22;
BC+AD=22-12=10;
MN=(BC+AD)/2 =10/2=5 см.
***
3. Пусть одно из оснований трапеции равно BC= х см. Тогда второе основание равно AD= х-10 см.
Средняя линия трапеции MN=(BC+AD)/2=13;
(x+x-10)/2=13;
2x-10=26;
2x=36;
ВС=x=18 большее основание;
AD=x-10=18-10=8 см - меньшее основание.
***
4. ∠BAC=CAD=∠BCA, как накрест лежащие при параллельных прямых BC и AD и секущей АС. Следовательно Δ АВС равнобедренный и стороны АВ=CD=ВС=7 см.
ответ: 18
Объяснение:
Параллельные плоскости пересекаются третьей плоскостью по параллельным прямым.
1. Плоскости граней AA₁D₁D и ВВ₁С₁С параллельны. Они пересечены плоскостью (АВ₁С₁), значит линии пересечения параллельны.
(АВ₁С₁) ∩ (ВВ₁С₁) = В₁С₁,
В₁С₁ ║ВС и ВС║AD как противолежащие стороны прямоугольников, ⇒ В₁С₁ ║ AD. Тогда
(АВ₁С₁) ∩ (АА₁D₁) = AD.
AB₁C₁D - сечение параллелепипеда плоскостью (АВ₁С₁).
2. Секущая плоскость и плоскость (АВ₁С₁) параллельны, значит они пересекаются плоскостями граней параллелепипеда по параллельным прямым.
Проведем МТ║AD, MK║DC₁, TP║AB₁ и PK║B₁C₁.
MKPT - искомое сечение.
3. ТМ║ВС, ВТ║СМ, ∠ТВС = 90°, значит ТВСМ прямоугольник,
ТМ = ВС = 4.
Аналогично, РК = ВС = 4.
МКРТ - параллелограмм, так как МТ║РК и МТ = РК.
М - середина CD, МК║DC₁, значит МК - средняя линия ΔDCC₁, тогда К - середина СС₁.
ΔМКС: ∠МСК = 90°, МС = CD/2 = 4, СК = СС₁/2 = 3, значит МК = 5 (египетский треугольник).
Pmkpt = 2(TM + MK) = 2 · (4 + 5) = 2 · 9 = 18
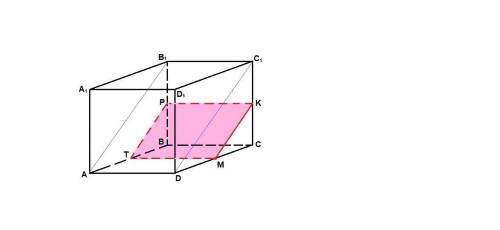
ответ на фото..........