плз) ,_, 2. Отрезки AB и CD пересекаются в точке O, являющейся их серединой. Известно также что угол ACD = углу BCD. Докажите, что треугольник BCD равнобедренный.
3. Докажите, что прямые AB и CD из предыдущего упражнения перпендикулярны.
4. Докажите, что если медиана треугольника является его биссектрисой, то он равнобедренный.
(ノT_T)ノ ^┻━┻
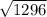 =36
=36
МА = 12 - расстояние от М до α,
МВ = 16 - расстояние от М до β.
Пусть плоскость АМВ пересекает ребро двугранного угла - прямую а - в точке С.
МА⊥α, а⊂α, значит МА⊥а.
МВ⊥β, а⊂β, значит МВ⊥а.
Так как прямая а перпендикулярна двум пересекающимся прямым плоскости АМВ, то она перпендикулярна этой плоскости, следовательно она перпендикулярна каждой прямой, лежащей в этой плоскости, ⇒
а⊥АС, а⊥ВС, ⇒∠АСВ = 90° - линейный угол двугранного угла;
а⊥МС, ⇒ МС - искомое расстояние.
МАСВ - прямоугольник, АС = МВ = 16.
Из прямоугольного треугольника АМС по теореме Пифагора:
МС = √(МА² + АС²) = √(16² + 12²) = √(256 + 144) = √400 = 20