
Заданное уравнение x^2+3x+y=0 определяет параболу (λ2 = 0)
Выделяем полные квадраты:
(x^2+2·(3/2)x + (3/2)^2) -1·(3/2)^2 = (x+(3/2))^2-(9/4 ).
Преобразуем исходное уравнение:
(x+(3/2))^2 = -y + (9/4).
Получили уравнение параболы:
(x - x0)2 = 2p(y - y0) .
(x-(-3/2))^2 = 2·(-1/2)(y - (9/4) ).
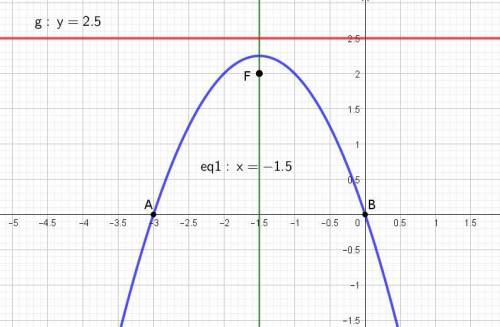
Ветви параболы направлены вниз (p<0), вершина расположена в точке (x0, y0), т.е. в точке (-3/2; (9/4) ).
Параметр p = -1/2
Координаты фокуса: F((-3/2); 2).
Уравнение директрисы: y = y0 - (p/2 )
y = (9/4) - (-1/4) = 5/2
Детальнее параметры кривой даны во вложении.

Объяснение:
Определение
Геометрическим местом точек (сокращенно — ГМТ), обладающих некоторым свойством, называется множество всех точек, которые обладают этим свойством.
Решение задачи на поиск ГМТ должно содержать доказательство того, что все точки множества , указанного в ответе, обладают требуемым свойством, а также наоборот, что все точки, обладающие требуемым свойством, лежат в этом множестве .
Приведем классические и важнейшие известные примеры ГМТ.
Пример
Геометрическое место точек, удаленных от данной точки на заданное положительное расстояние, — окружность (это определение окружности).
Пример
Геометрическое место точек, равноудаленных от данной прямой, — две параллельные прямые.
Пример
Геометрическое место точек, равноудаленных от концов отрезка, — серединный перпендикуляр к отрезку.
Пример
Геометрическое место внутренних точек угла, равноудаленных от его сторон, — биссектриса угла.
Два последних примера будут рассмотрены детально в разделах "Серединный перпендикуляр" и "Биссектриса".
Утверждение
ГМТ, обладающих двумя свойствами, является пересечением двух множеств: ГМТ, обладающих первым свойством, и ГМТ, обладающих, вторых свойств
Длина параллелограмма
стороны параллелограмма
сторона ромба
ДИАГОНАЛЬ ПРЯМОУГОЛЬНИКА