Угол ABC = 30гр
Угол DAB = 45 гр
Объяснение:
Решаем через синусы прямоугольных треугольников.
В треугольнике ACB угол С - прямой.
Синус прямоугольного треугольника равен отношению противолежащего этому углу катета к гипотенузе.
То есть синус ABC = 6 см / 12 см = 1/2
Смотрим таблицу синусов - 1/2 у угла 30 гр
---
В треугольнике ADB угол D прямой
Синус прямоугольного треугольника равен отношению противолежащего этому углу катета к гипотенузе.
Синус угла DAB = BD/AB = 6√2 см/12 см = √2/2
Смотрим таблицу синусов - такой синус у угла 45 гр
---
Объяснение:
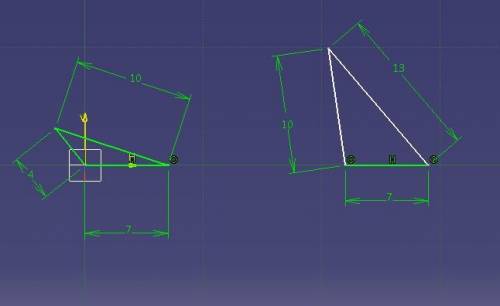
4,7,10,13 см длины проволок.
1. Основное правило существования треугольников: сумма двух любых сторон должна быть больше, чем третья сторона (если нарисовать треугольник, это хорошо видно. Крайний случай, когда один из углов треугольника почти равен 180 град).
Из этого правила.
Возьмем проволоки 4, 7 и 13 cм. Тогда
4+7=11 < 13 (т.е. сумма сторон меньше 3ей, поэтому такого треугольника быть не может)
Возьмем проволоки 4, 7, 10. Тогда
4+7=11 > 10
7+10=17 > 4
4+10=14 > 7
Правило выполняется для любой из сторон, следовательно треугольник существует.
Из проволок можно собрать еще 2 треугольника
{4,10,13}, {7,10,13}, но для них правило выполняется, значит они существуют. Рисунки 2х прикрепил к ответу
Апофема правильной треугольной пирамиды равна 9/√π, двугранный угол при ребре основания 60°. Вычислите площадь сферы вписанной в пирамиду.
Вспомним, что правильной называется пирамида, в основании которой лежит правильный треугольник.
Поскольку пирамида правильная, в нее можно вписать шар.
Его центр лежит на высоте пирамиды и совпадает с центром окружности, вписанной в треугольник, боковые стороны которого равны апофеме. ( См. рисунок)
Так как двугранный угол этой пирамиды равен 60°, то и основание треугольника MSH равно апофеме пирамиды. Т.е. треугольник этот - равносторонний.
Радиус сферы, площадь поверхности которой предстоит найти, равен радиусу вписанной в этот равносторонний треугольник окружности и равен одной трети высоты этого треугольника, которая является и высотой пирамиды.
Эту высоту найдем из треугольника SOM.
Она равна SM·sin (60°)
SO=(9/√π)·(√3):2
Радиус вписанной сферы в эту пирамиду
r=(3√3):2√π
S=4πR²
S=4π{(3√3):2√π}²=4π·27:4π=27 см²