Как-то так :)
а) 180-100-40=40 (треугольник равно бедренный, так-как две стороны из трех равны)
б) образует два новых прямых угла точно, но по поводу острых не уверена.
Объяснение:
центр описанной окружности в остроугольном и тупоугольном треугольнике - точка пересечения их серединных перпендикуляров.
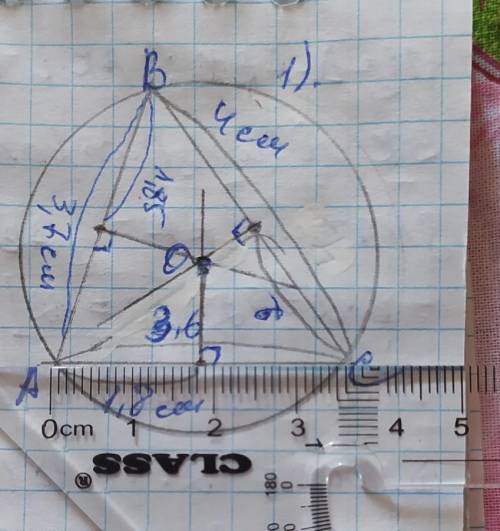
1) Рисуем остроугольный треугольник, измеряем каждую сторону, делим эту величину на 2 и отмечаем точкой середину отрезка. АС=3,6см, значит середина отрезка АС=3,6÷2=1,8см. Отметив эту точку, с угольника проведём к ней перпендикуляр.
Так проделываем с другими двумя сторонами.
Отмечаем точку пересечения перпендикуляров О и фиксируем на ней острую ножку циркуля. Радиус описанной окружности - это расстояние от центра окружности к любой вершине треугольника.
Обозначив радиус, описываем окружность.
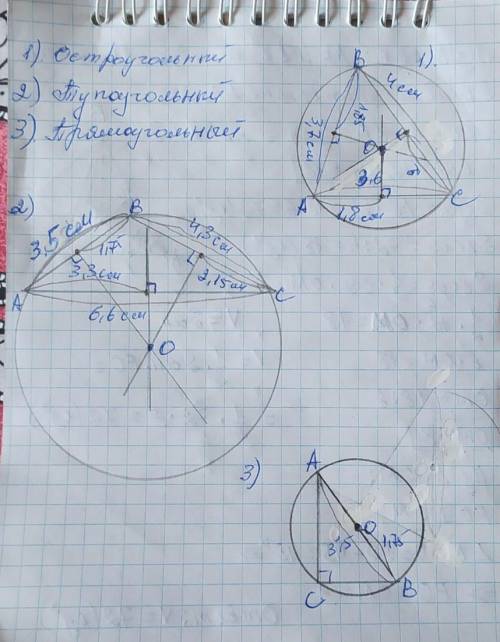
2) То же проделываем с тупоугольном треугольником. Только в тупоугольном треугольнике точка пересечения перпендикуляров находится вне его.
3) В прямоугольном треугольнике центром окружности является середина гипотенузы АВ.
Находим в ней середину по тому же принципу, что и в предыдущих треугольниках и радиусом будет расстояние от центра окружности до любой вершины треугольника. В данном случае гипотенуза равна 3,5см, тогда расстояние от точки О до вершины=3,5÷2=1,75см.



Ну тк. один угол 100 градусов, а другой 40, мы найдем еще один угол, сумма углов в тр-ке 180 градусов 180-40=40. У нас получается два равных угла, следовательно треугольник равнобедренный. АB и AC его обоковые стороны.
Теперь следующее, нам нужно найти какие углы биссектриса СК образует с стороной АВ, ну тк биссектриса делит угол на два равных а угол С=40 градусов то углы образованные ей будут равны 20 градусов, дальше рассмотрим два треугольника, один из двух, допустим АСК у нас есть один угол 100 градусов и 20, надем угол акс 180-120=60. ну и укглы АКС и ВКС смежные и их сумма равна 180 градусов ну и отнимаем из 180 60 и получаем 120 т.е. 1 угол 60 2 120.