ΔABC - равнобедренный;
высота BD = 6,4 см;
AB = BC = 12,8 см.
Найти:∠A = ?°; ∠B = ?°; ∠C = ?°.
Решение:Высота, проведённая к основанию равнобедренного треугольника, является и медианой, и биссектрисой.
⇒ AD = DC, ∠ABD = ∠BDC (по выше указанному свойству).
⇒ ΔABD = ΔCBD (по двум сторонам и углу между ними).
Нам также известно что равные треугольники прямоугольные (высота BD).
Если катет равен половине гипотенузы, то напротив лежащий угол составляет 30°.
Боковые стороны равнобедренного ΔABC - гипотенузы прямоугольных ΔABD и ΔСBD, а высота - общий катет.
Как мы уже отметили, этот общий катет равен половине гипотенузы, так как 6,4 * 2 = 12,8 см. Поэтому ∠A = ∠C = 30°.
Сумма острых углов в прямоугольном треугольнике равна 90°.
⇒ ∠ABD = ∠CBD = 90° - 30° = 60°. ⇒ ∠B = 120°.
ответ: ∠A = ∠C = 30°, ∠B = 120°.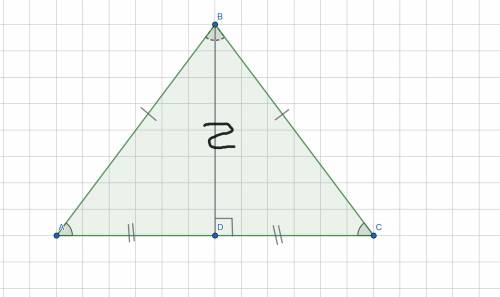
Обозначим вершины трапеции АBCD AD=20 BC=12.
проведём диагональ АС и опустим высоту СН. Трапеция равнобокая DН=(АD-BC)/2=4
AC пересекает параллельные прямые АD и BC поэтому накрест лежащие углы равны . угол САD равен углу АСВ. Кроме того СА биссектриса угла ВСD . Поэтому CAD также равен углу АСD. рассмотрим треугольник АСD. В нем мы только что установили что угол А равен углу С. Поэтому АD равно DC = 20.
теперь рассмотрим треугольник СНD. он прямоугольный . угол Н прямой. DC=20 DH=4 по теореме Пифагора CH = √(20^2-4^2)= 8√6.
Площадь трапеции - средняя линия (АD+BC)/2= 16 умножить на найденную высоту СН=8√6 - равна 128√6